题目内容
已知函数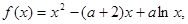
(1)求函数的单调区间与极值点;
(2)若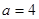 ,方程
,方程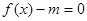 有三个不同的根,求
有三个不同的根,求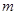 的取值范围。
的取值范围。
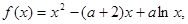
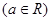
(1)求函数的单调区间与极值点;
(2)若
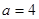 ,方程
,方程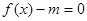 有三个不同的根,求
有三个不同的根,求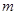 的取值范围。
的取值范围。1) 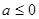 时,
时,  的递减区间为
的递减区间为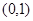 ,递增区间为
,递增区间为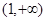 ;极小值点为1,无极大值点.
;极小值点为1,无极大值点.
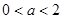 时,
时, 的递减区间为
的递减区间为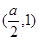 ,递增区间为
,递增区间为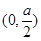 和
和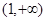 ;极小值点为1,极大值点为
;极小值点为1,极大值点为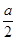 .
.
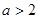 时,
时, 的递减区间为
的递减区间为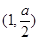 ,递增区间为
,递增区间为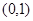 和
和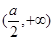 ;极小值点为
;极小值点为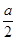 ,极大值点为1.
,极大值点为1.
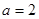 时,
时,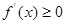 ,
, 在
在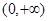 递增,无减区间,无极值点。
递增,无减区间,无极值点。
(2)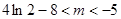
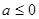 时,
时,  的递减区间为
的递减区间为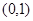 ,递增区间为
,递增区间为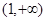 ;极小值点为1,无极大值点.
;极小值点为1,无极大值点.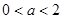 时,
时, 的递减区间为
的递减区间为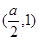 ,递增区间为
,递增区间为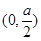 和
和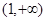 ;极小值点为1,极大值点为
;极小值点为1,极大值点为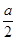 .
.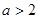 时,
时, 的递减区间为
的递减区间为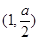 ,递增区间为
,递增区间为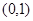 和
和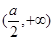 ;极小值点为
;极小值点为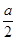 ,极大值点为1.
,极大值点为1.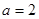 时,
时,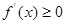 ,
, 在
在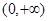 递增,无减区间,无极值点。
递增,无减区间,无极值点。(2)
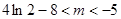
本试题主要是考查了导数在研究函数中的运用。
(1)根据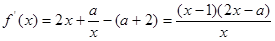 , 令
, 令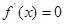 得
得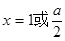
对于a分情况讨论得到单调性和极值。
(2)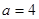 时,
时,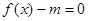 即
即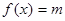 ,
,
由(1)可知,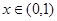 时
时 递增,
递增,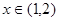 时
时 递减,
递减,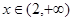 时
时 递增;
递增;
极大值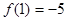 ,极小值
,极小值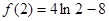
要使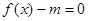 有三个不同的根,则
有三个不同的根,则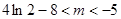
1)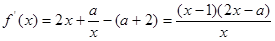 , 令
, 令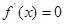 得
得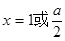
当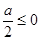 即
即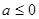 时,
时,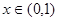 时,
时,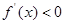 ;
;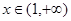 时;
时;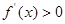
∴ 的递减区间为
的递减区间为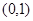 ,递增区间为
,递增区间为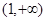 ;极小值点为1,无极大值点.
;极小值点为1,无极大值点.
当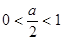 即
即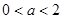 时,
时,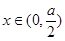 时,
时,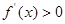 ;
;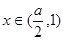 时,
时,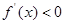 ;
;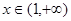 时,
时,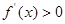 ;
;
∴ 的递减区间为
的递减区间为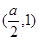 ,递增区间为
,递增区间为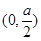 和
和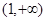 ;极小值点为1,极大值点为
;极小值点为1,极大值点为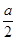 .
.
当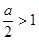 即
即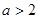 时,
时,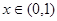 时,
时,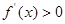 ;
;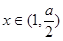 时,
时,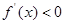 ;
;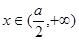 时,
时,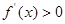 ;
;
∴ 的递减区间为
的递减区间为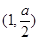 ,递增区间为
,递增区间为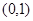 和
和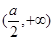 ;极小值点为
;极小值点为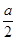 ,极大值点为1.
,极大值点为1.
当 即
即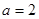 时,
时,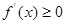 ,
, 在
在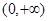 递增,无减区间,无极值点。
递增,无减区间,无极值点。
(2)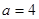 时,
时,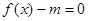 即
即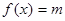 ,
,
由(1)可知,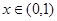 时
时 递增,
递增,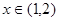 时
时 递减,
递减,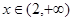 时
时 递增;
递增;
极大值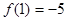 ,极小值
,极小值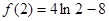
要使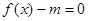 有三个不同的根,则
有三个不同的根,则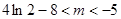
(1)根据
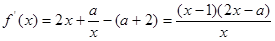 , 令
, 令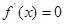 得
得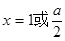
对于a分情况讨论得到单调性和极值。
(2)
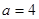 时,
时,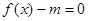 即
即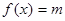 ,
, 由(1)可知,
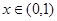 时
时 递增,
递增,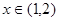 时
时 递减,
递减,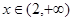 时
时 递增;
递增;极大值
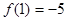 ,极小值
,极小值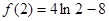
要使
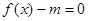 有三个不同的根,则
有三个不同的根,则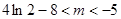
1)
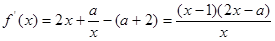 , 令
, 令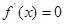 得
得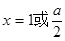
当
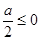 即
即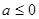 时,
时,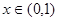 时,
时,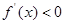 ;
;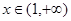 时;
时;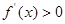
∴
 的递减区间为
的递减区间为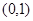 ,递增区间为
,递增区间为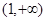 ;极小值点为1,无极大值点.
;极小值点为1,无极大值点.当
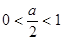 即
即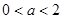 时,
时,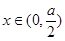 时,
时,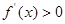 ;
;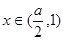 时,
时,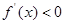 ;
;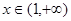 时,
时,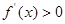 ;
;∴
 的递减区间为
的递减区间为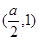 ,递增区间为
,递增区间为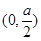 和
和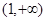 ;极小值点为1,极大值点为
;极小值点为1,极大值点为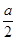 .
.当
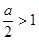 即
即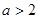 时,
时,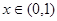 时,
时,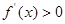 ;
;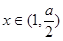 时,
时,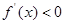 ;
;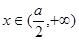 时,
时,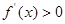 ;
;∴
 的递减区间为
的递减区间为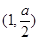 ,递增区间为
,递增区间为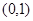 和
和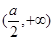 ;极小值点为
;极小值点为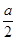 ,极大值点为1.
,极大值点为1.当
 即
即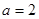 时,
时,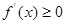 ,
, 在
在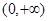 递增,无减区间,无极值点。
递增,无减区间,无极值点。(2)
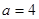 时,
时,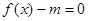 即
即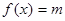 ,
, 由(1)可知,
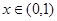 时
时 递增,
递增,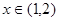 时
时 递减,
递减,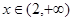 时
时 递增;
递增;极大值
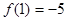 ,极小值
,极小值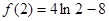
要使
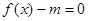 有三个不同的根,则
有三个不同的根,则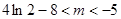

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .(Ⅰ) 求
.(Ⅰ) 求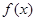 在
在 上的最小值;(Ⅱ) 若存在
上的最小值;(Ⅱ) 若存在 (
( 是常数,
是常数, )使不等式
)使不等式 成立,求实数
成立,求实数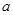 的取值范围;
的取值范围; 都有
都有 成立.
成立.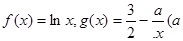 为实常数).
为实常数).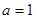 时,求函数
时,求函数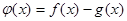 在
在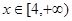 上的最小值;
上的最小值;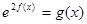 在区间
在区间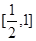 上有解,求实数
上有解,求实数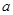 的取值范围;
的取值范围;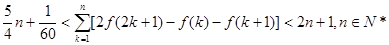
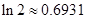 )
) 在点
在点 的切线方程为
的切线方程为 .
. 的解析式;
的解析式; ,求证:
,求证: 在
在 上恒成立.
上恒成立.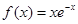 (x∈R).
(x∈R).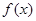 的单调区间和极值;
的单调区间和极值; 的图象与函数
的图象与函数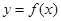 的图象关于直线x=1对称,证明当x>1时,
的图象关于直线x=1对称,证明当x>1时,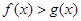 .
. 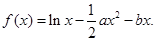
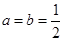 时,求函数
时,求函数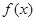 的最大值;
的最大值;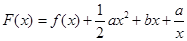 ,(
,(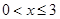 )其图象上任意一点
)其图象上任意一点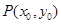 处切线的斜率
处切线的斜率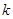 ≤
≤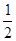 恒成立,求实数
恒成立,求实数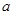 的取值范围;
的取值范围;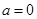 ,
,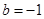 ,方程
,方程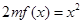 有唯一实数解,求正数
有唯一实数解,求正数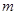 的值.
的值.  是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式 的解集是:
的解集是: (2,+
(2,+  )
) .(
.(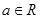 ).
).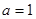 时,求函数
时,求函数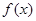 的极值;
的极值;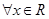 ,有
,有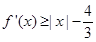 成立,求实数
成立,求实数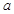 的取值范围.
的取值范围.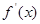 是函数
是函数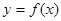 的导函数,且
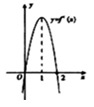
的导函数,且 的图像如图所示,
的图像如图所示,