题目内容
正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为 a.
a.

(1)建立适当的坐标系,并写出A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
 a.
a.
(1)建立适当的坐标系,并写出A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
(1) A(0,0,0),B(0,a,0),A1(0,0, a),C1(-
a),C1(-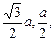
 a) ,(2) AC1与侧面ABB1A1所成的角为30°
a) ,(2) AC1与侧面ABB1A1所成的角为30°
 a),C1(-
a),C1(-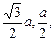
 a) ,(2) AC1与侧面ABB1A1所成的角为30°
a) ,(2) AC1与侧面ABB1A1所成的角为30° (1)以点A为坐标原点O,以AB所在直线为Oy轴,以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知,得A(0,0,0),B(0,a,0),A1(0,0, a),C1(-
a),C1(-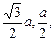
 a).
a).
(2)取A1B1的中点M,于是有M(0,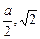 a),连AM,MC1,
a),连AM,MC1,
有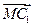 =(-
=(-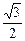 a,0,0),且
a,0,0),且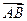 =(0,a,0),
=(0,a,0),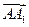 =(0,0
=(0,0 a)
a)
由于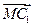 ·
·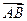 =0,
=0,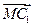 ·
·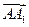 =0,所以MC1⊥面ABB1A1,
=0,所以MC1⊥面ABB1A1,
∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵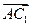 =
=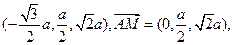
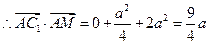
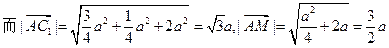
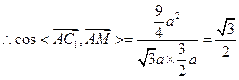
所以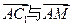 所成的角,即AC1与侧面ABB1A1所成的角为30°.
所成的角,即AC1与侧面ABB1A1所成的角为30°.
由已知,得A(0,0,0),B(0,a,0),A1(0,0,
 a),C1(-
a),C1(-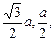
 a).
a).(2)取A1B1的中点M,于是有M(0,
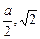 a),连AM,MC1,
a),连AM,MC1,有
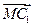 =(-
=(-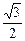 a,0,0),且
a,0,0),且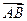 =(0,a,0),
=(0,a,0),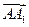 =(0,0
=(0,0 a)
a)由于
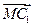 ·
·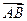 =0,
=0,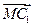 ·
·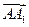 =0,所以MC1⊥面ABB1A1,
=0,所以MC1⊥面ABB1A1,∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵
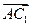 =
=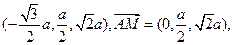
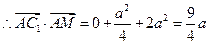
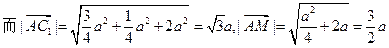
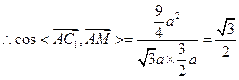
所以
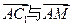 所成的角,即AC1与侧面ABB1A1所成的角为30°.
所成的角,即AC1与侧面ABB1A1所成的角为30°.
练习册系列答案
相关题目
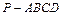 中,
中,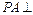 底面
底面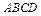 ,
,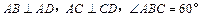 ,
,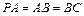 ,
, 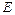 是
是 的中点.
的中点. (1)证明
(1)证明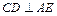 ;
;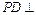 平面
平面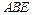 ;
;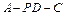 的大小.
的大小.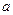 .
.

 中,
中, 底面
底面 ,
, ,
,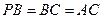 ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
 ;(2)求二面角
;(2)求二面角 的余弦值。
的余弦值。