题目内容
已知点O在二面角α-AB-β的棱上,点P在α内,且∠POB=45°.若对于β内异于O的任意一点Q,都有∠POQ≥45°,则二面角α-AB-β的取值范围是_________.

若二面角α-AB-β的大小为锐角,则过点P向平面 作垂线,设垂足为H.
作垂线,设垂足为H.
过H作AB的垂线交于C,连PC、CH、OH,则 就是所求二面角的平面角. 根据题意得
就是所求二面角的平面角. 根据题意得 ,由于对于β内异于O的任意一点Q,都有
,由于对于β内异于O的任意一点Q,都有
∠POQ≥45°,∴ ,设PO=
,设PO= ,则
,则
又∵∠POB=45°,∴OC=PC= ,而在
,而在 中应有
中应有
PC>PH ,∴显然矛盾,故二面角α-AB-β的大小不可能为锐角。
即二面角 的范围是
的范围是 。
。

 作垂线,设垂足为H.
作垂线,设垂足为H.过H作AB的垂线交于C,连PC、CH、OH,则
 就是所求二面角的平面角. 根据题意得
就是所求二面角的平面角. 根据题意得 ,由于对于β内异于O的任意一点Q,都有
,由于对于β内异于O的任意一点Q,都有∠POQ≥45°,∴
 ,设PO=
,设PO= ,则
,则
又∵∠POB=45°,∴OC=PC=
 ,而在
,而在 中应有
中应有PC>PH ,∴显然矛盾,故二面角α-AB-β的大小不可能为锐角。
即二面角
 的范围是
的范围是 。
。

练习册系列答案
相关题目
 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
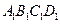 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为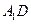 、A1C的中点.
、A1C的中点.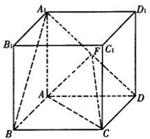
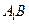 ∥平面AFC;.
∥平面AFC;.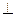 平面AFC.
平面AFC. a.
a.
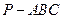 高为2,侧棱与底面所成角为
高为2,侧棱与底面所成角为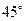 ,则点
,则点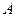 到侧面
到侧面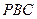 的距离是
的距离是



 ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
 的六条棱长分别为
的六条棱长分别为 ,且知
,且知 ,则
,则 .
.
 、
、 ;
;  、
、 ;
;  、
、 ;
;  、
、 .
.