Question

【题目】已知椭圆C： （a＞b＞0）的离心率为 ，左、右焦点分别为F1 ， F2 ， 点G在椭圆C上，且 =0，△GF1F2的面积为2．

（1）求椭圆C的方程；
（2）直线l：y=k（x﹣1）（k＜0）与椭圆Γ相交于A，B两点．点P（3，0），记直线PA，PB的斜率分别为k1 ， k2 ， 当 最大时，求直线l的方程．

Answer 1

【答案】
（1）解：∵椭圆 （a＞b＞0）的离心率为 ，

∴e= ，①

∵左右焦点分别为F1、F2，点G在椭圆上，

∴| |+| |=2a，②

∵ =0，△GF1F2的面积为2，

∴| |2+| |2=4c2，③

，④

联立①②③④，得a2=4，b2=2，

∴椭圆C的方程为 ；

（2）解：联立 ，得（1+2k2）x2﹣4k2x+2k2﹣4=0．

设A（x1，y1），B（x2，y2），

∴ ．

= =

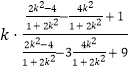= ，当且仅当 时，取得最值．

此时l：y=

【解析】（1）由椭圆的离心率为 、点G在椭圆上、 =0及△GF1F2的面积为2列式求得a2=4，b2=2，则椭圆方程可求；（2）联立直线方程和椭圆方程，化为关于x的一元二次方程，利用根与系数的关系得到A，B两点横坐标的和与积，把 转化为含有k的代数式，利用基本不等式求得使 取得最大值的k，则直线Γ的方程可求．
【考点精析】根据题目的已知条件，利用椭圆的标准方程的相关知识可以得到问题的答案，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：．