题目内容
如图,在长方体?ABCD—A1B1C1D1中,?AB=AA1=a,BC=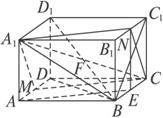
(1)求证:A1、M、C、N四点共面;
(2)求证:BD1⊥CM;
(3)求A1B和平面A1MCN所成角的大小.
(1)证明:如图,取BC的中点E,可证AECM是平行四边形;

AENA1也是平行四边形;由CM∥AE∥A1N,可证A1、M、C、N四点共面.
(2)证明:连结BD,
在Rt△CDM和Rt△BCD中,![]() ,
,
∴Rt△CDM∽Rt△BCD,可证BD⊥CM,
∵BD是BD1在底面ABCD上的射影,
∴BD1⊥CM.
(3)解:连结BC1,同样可以证明BC1⊥CN.
∵BC1是BD1在侧面BCC1B1上的射影,
∴BD1⊥CN.
∵CN∩CM=C,
∴BD1⊥平面A1MCN.
连结A1C,交BD1于F,则A1F是A1B在平面A1MCN上的射影,则∠BA1F即是A1B和平面A1MCN所成的角,
∵tan∠BA1C=![]() .∴∠BA1F=45°.
.∴∠BA1F=45°.

练习册系列答案
相关题目
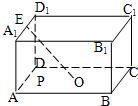 例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )
例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )A、离心率为
| ||||
B、离心率为
| ||||
| C、一段抛物线 | ||||
| D、半径等于1的圆 |
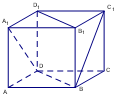 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,A1D与BC1所成角为90°,则直线BC1与平面BB1D1D所成角的大小为
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,A1D与BC1所成角为90°,则直线BC1与平面BB1D1D所成角的大小为 如图,在长方体AC1中,AB=BC=2,
如图,在长方体AC1中,AB=BC=2, (2010•台州二模)如图,在长方体ABCD-A1B1C1D1中,AB=10,AD=5,AA1=4.分别过BC、A1D1的两个平行截面将长方体分成 三部分,其体积分别记为V1=
(2010•台州二模)如图,在长方体ABCD-A1B1C1D1中,AB=10,AD=5,AA1=4.分别过BC、A1D1的两个平行截面将长方体分成 三部分,其体积分别记为V1=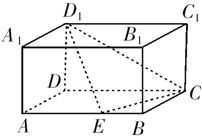 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,