题目内容
已知函数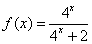 .(Ⅰ)求
.(Ⅰ)求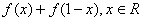 的值;
的值;
(Ⅱ)若数列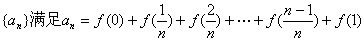
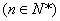 ,求数列
,求数列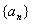 的通项公式;
的通项公式;
(Ⅲ)若数列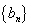 满足
满足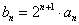 ,
,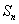 是数列
是数列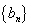 的前
的前 项和,是否存在正实数
项和,是否存在正实数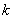 ,使不等式
,使不等式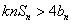 对于一切的
对于一切的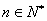 恒成立?若存在,请求出
恒成立?若存在,请求出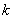 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(1) =
= +
+ =
= +
+ =1
=1
(2)∵ ①
①
∴ ②
②
由(Ⅰ),知 =1
=1
∴①+②,得
(3)∵ 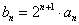 ,∴
,∴ 
∴ , ①
, ①
 , ②
, ②
①-②得
即 要使得不等式
要使得不等式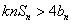 恒成立,即
恒成立,即 对于一切的
对于一切的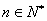 恒成立,
恒成立,
法一: 对一切的
对一切的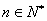 恒成立,
恒成立,
令 ,
,
∵ 在
在 是单调递增的, ∴
是单调递增的, ∴ 的最小值为
的最小值为
∴ =
= , ∴
, ∴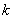

 .
.
法二:  . 设
. 设
当 时,由于对称轴直线
时,由于对称轴直线
 ,且
,且
 ,而函数
,而函数 在 是增函数, ∴不等式
在 是增函数, ∴不等式 恒成立
恒成立
即当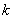

 时,不等式
时,不等式 对于一切的
对于一切的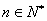 恒成立.
恒成立.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
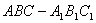 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是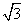 ,D是AC的中点。
,D是AC的中点。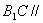 平面
平面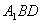 ;
;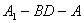 的大小;
的大小; 与平面
与平面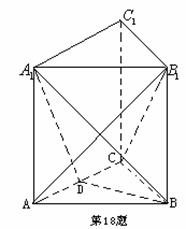
 恒成立,则实数a的取值范围是 。
恒成立,则实数a的取值范围是 。 :
: ,若不等式
,若不等式 对任意实数
对任意实数 成立,则a的取值范围为 ( )
成立,则a的取值范围为 ( ) B.
B. C.
C. D.
D.
 分别为角
分别为角 所对的边,
所对的边, 的大小; (2)若
的大小; (2)若 的最大值。
的最大值。 ( )
( )  的图像关于
的图像关于 轴对称,则此函数的图象与
轴对称,则此函数的图象与 C.2 D.4
C.2 D.4 服从正态分布
服从正态分布 ,且
,且 上取值的概率为0.8,则
上取值的概率为0.8,则 等于( )
等于( ) B.
B.
 D.
D.