题目内容
12.若函数f(x)=x3+2x-1的零点在区间(k,k+1)(k∈Z)内,则k=0.分析 利用根的存在性确定函数零点所在的区间,然后确定k的值.
解答 解;∵f(x)=x3+2x-1,
∴f′(x)=3x2+2>0,
∴f(x)在R上单调递增,
∵f(0)=-1<0,f(1)=1+2-1>0,
∴f(0)f(1)<0,
∴函数零点所在的区间为(0,1),
∴k=0.
故答案为:0.
点评 本题考查函数零点的判定定理的应用,属基础知识、基本运算的考查.

练习册系列答案
相关题目
2.已知正项数列{an}满足a${\;}_{n+1}^{2}$=9an2,若a5a6=8,则a4a7+a5a7=( )
| A. | 32 | B. | 80 | C. | -16或32 | D. | -64或80 |
20.把函数y=sin(4x+φ)图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有的点向右平$\frac{π}{3}$个单位,所得图象关于y轴对称,则φ的一个可能值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
4.下列各式中正确的是( )
| A. | -$\sqrt{x}$=(-x)${\;}^{\frac{1}{2}}$ | B. | x${\;}^{-\frac{1}{5}}$=-$\root{5}{x}$ | C. | (-x)${\;}^{\frac{2}{3}}$=x${\;}^{\frac{2}{3}}$ | D. | x${\;}^{\frac{2}{6}}$=x${\;}^{\frac{1}{3}}$ |
1.函数f(x)=$\frac{lg(x+2)}{x-1}$的定义域是( )
| A. | (-2,1) | B. | [-2,1)∪(1,+∞) | C. | (-2,+∞) | D. | (-2,1)∪(1,+∞) |
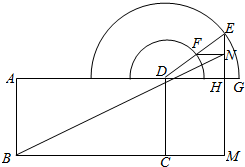 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.