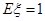题目内容
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题:①
 在
在 内单调递增;
内单调递增;②
 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;③
 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;④
 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
C
试题分析:(1)
 =
=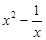 ,
,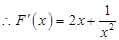 ,则
,则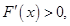 解得
解得 ,所以
,所以 在
在 内单调递增;故①正确.
内单调递增;故①正确.(2)
 和
和 之间存在“隔离直线”,设“隔离直线”为
之间存在“隔离直线”,设“隔离直线”为 ,当“隔离直线”与
,当“隔离直线”与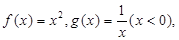 同时相切时,截距最小,令切点坐标为
同时相切时,截距最小,令切点坐标为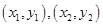 ,则切线方程为
,则切线方程为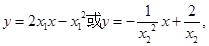 所以
所以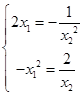 ,故
,故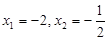 ,所以
,所以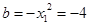 ,此时截距最小,故②正确;此时斜率为
,此时截距最小,故②正确;此时斜率为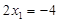 ,k的取值范围是
,k的取值范围是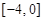 .故③错误.
.故③错误.④令F(x)=h(x)-m(x)=x2-2elnx(x>0),再令F′(x)═
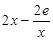 =0,x>0,得x=
=0,x>0,得x=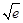 ,
,从而函数h(x)和m(x)的图象在x=
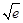 处有公共点.
处有公共点.因此存在h(x)和m(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则
隔离直线方程为y-e=k(x-
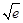 ),即y=kx-k
),即y=kx-k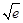 +e.
+e.由h(x)≥kx-k
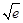 +e可得 x2-kx+k
+e可得 x2-kx+k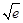 -e≥0当x∈R恒成立,
-e≥0当x∈R恒成立,则△=k2-4k
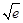 +4e=
+4e=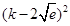 ≤0,只有k=2
≤0,只有k=2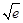 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2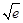 x-e.
x-e.同理证明,由φ(x )≤kx-k
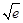 +e,可得只有k=2
+e,可得只有k=2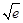 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2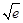 x-e.
x-e.综上可得,函数f(x)和g(x)存在唯一的隔离直线y=2
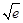 x-e,故④正确.
x-e,故④正确.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 函数
函数 在区间
在区间 上是单调递增函数;命题
上是单调递增函数;命题 不等式
不等式 对任意实数
对任意实数 恒成立.若
恒成立.若 是真命题,且
是真命题,且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. ;
; ,若
,若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围.
的取值范围.

 ,
, ”的否定为 .
”的否定为 .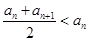 ,
,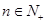 ,则
,则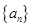 为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( ) :
: ,命题
,命题 :
: (
( ).
). ”是“
”是“ ”的必要而不充分条件,求实数
”的必要而不充分条件,求实数 的取值范围.
的取值范围. ”是“
”是“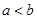 ”的充分不必要条件
”的充分不必要条件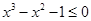 对
对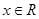 恒成立”的否定是“存在
恒成立”的否定是“存在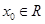 使得
使得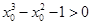 ”
”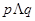 ”为假命题,则
”为假命题,则 均为假命题
均为假命题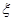 服从二项分布:
服从二项分布: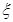 ~
~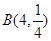 ,则
,则