Question

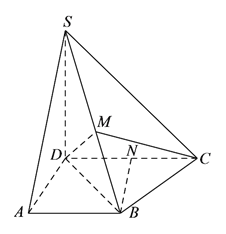
【题目】如图，在直角梯形中， ， ， 平面， ， ， 的中点为．

（）求证： 面．

（）求证：平面平面．

（）当为何值时，能使？请给出证明．

Answer 1

【答案】证明见解析．

【解析】试题分析：（）在直角梯形中， ， 平面， 平面，易证平面．

（2）根据线面垂直的判定定理易证得AB⊥平面SAD，进而根据面面平行的判定定理易证得结论；

（3）分析可得当时，能使DM⊥MC，然后设CD的中点为P，连接BD，BP，再根据等腰三角形的性质易证得DM⊥SB，然后根据线面垂直的性质DM⊥BC，进而得到DM⊥平面SBC，从而证得结论.

试题解析：（）证明：∵在直角梯形中，

，

平面，

平面，

∴平面．

（）证明：∵，

平面，

∴，

∵点，

、平面，

∴平面，

又∵平面，

∴平面平面．

（）当时，有，

连接，

∵， ，

∴，

∴， ，

∵为中点，

∴，

设中点为，连接，且，

∴， ，

∵， ，

∴，即，

∴， ，

平面， ，

∵点，

∴平面，

∵平面，

∴，

∵点，

平面，

平面，

∴．