题目内容
幂函数y=f(x)的图象过点A(4,2),则函数y=f(x)的反函数f-1(x)=________(要求写明定义域).
y=x2(x≥0)
分析:先设幂函数f(x)=xα,根据条件求得指数即得原函数f(x),再求f(x)的反函数即得.解答本题首先熟悉反函数的概念,然后根据反函数求解三步骤:1、换:x、y换位,2、解:解出y,3、标:标出定义域,据此即可求得反函数.
解答:设幂函数f(x)=xα,
∵幂函数y=f(x)的图象过点A(4,2),
∴4α=2→α= ,
,
∴幂函数f(x)=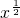 ,
,
则函数y=f(x)的反函数f-1(x)=x2(x≥0).
故答案为:y=x2(x≥0).
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).
分析:先设幂函数f(x)=xα,根据条件求得指数即得原函数f(x),再求f(x)的反函数即得.解答本题首先熟悉反函数的概念,然后根据反函数求解三步骤:1、换:x、y换位,2、解:解出y,3、标:标出定义域,据此即可求得反函数.
解答:设幂函数f(x)=xα,
∵幂函数y=f(x)的图象过点A(4,2),
∴4α=2→α=
 ,
,∴幂函数f(x)=
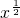 ,
,则函数y=f(x)的反函数f-1(x)=x2(x≥0).
故答案为:y=x2(x≥0).
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目