题目内容
在△ABC的三内角A,B,C所对的边分别为a,b,c,已知cosB=-| 5 |
| 13 |
| 4 |
| 5 |
(Ⅰ)求sinA的值;
(Ⅱ)设△ABC的面积为
| 33 |
| 2 |
分析:(Ⅰ)利用同角三角函数基本关系求出sinB和sinC,利用sinA=sin(B+C)=sinBcosC+cosBsinC 求出结果.
(Ⅱ) 利用三角形的面积公式求出 bc值,再用正弦定理求得b 值.
(Ⅱ) 利用三角形的面积公式求出 bc值,再用正弦定理求得b 值.
解答:解:(Ⅰ)∵cosB=-
,cosC=
,且A,B,C是三角形的内角,∴sinB=
,sinC=
.
∴sinA=sin(B+C)=sinBcosC+cosBsinC=
×
+(-
)×
=
.
(Ⅱ)∵S△ABC=
bcsinA=
,∴bc=65.∵
=
,
∴
=
,c=
b,解得:b=10.
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
∴sinA=sin(B+C)=sinBcosC+cosBsinC=
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 33 |
| 65 |
(Ⅱ)∵S△ABC=
| 1 |
| 2 |
| 33 |
| 65 |
| b |
| sinB |
| c |
| sinC |
∴
| b | ||
|
| c | ||
|
| 13 |
| 20 |
点评:本题考查同角三角函数基本关系,诱导公式、两角和的公式、正弦定理得应用,三角恒等变换是本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,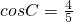 .
.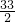 ,求b.
,求b. ,
, .
. ,求b.
,求b.