题目内容
复数z对应的点在第二象限,它的模为3,实部是-| 5 |
分析:设z=-
+bi,b>0,由它的模为3,解出b,可得z的共轭复数.
| 5 |
解答:解:设复数z的虚部为 b,则 z=-
+bi,b>0,
∵3=
,∴b=2,∴z=-
+2i,
则z的共轭复数是-
-2i,
故答案为-
-2i.
| 5 |
∵3=
| 5+b2 |
| 5 |
则z的共轭复数是-
| 5 |
故答案为-
| 5 |
点评:本题考查复数的共轭复数及复数的模的定义,求出复数z的虚部 b 是解题的关键.

练习册系列答案
相关题目
复数z对应的点在第二象限,|z|=3,实部是-
,则
是( )
| 5 |
. |
| z |
A、-
| ||
B、-
| ||
| C、A={(x,y)|x+3y=7+2i} | ||
| D、B={(x,y)|x-y=-1-2i| |
复数z对应的点在第二象限,它的模为3,实部是-
,则
是( )
| 5 |
. |
| z |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
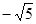 ,则
,则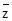 是 ( )
是 ( ) 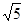 +2i D.
+2i D.