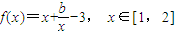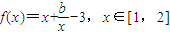题目内容
已知
(1)b=2时,求f(x)的值域;
(2)b≥2时,f(x)>0恒成立,求b的取值范围.
解:(1)当b=2时,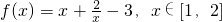 .
.
因为f(x)在 上单调递减,在
上单调递减,在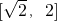 上单调递增,
上单调递增,
所以f(x)的最小值为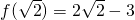 .
.
又因为f(1)=f(2)=0,
所以f(x)的值域为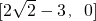 .
.
(2)(ⅰ)当2≤b<4时,因为f(x)在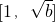 上单调递减,在
上单调递减,在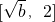 上单调递增,
上单调递增,
f(x)最小值为 ,f(x)>0,即
,f(x)>0,即 .
.
得 .
.
(ⅱ)b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为 ,f(x)>0,
,f(x)>0,
即 ,得b>2,因此b≥4.
,得b>2,因此b≥4.
综合(ⅰ)(ⅱ)可知 .
.
分析:(1)当b=2时,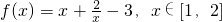 ,利用双钩函数的单调性即可求得f(x)的值域;
,利用双钩函数的单调性即可求得f(x)的值域;
(2))b≥2时,f(x)>0恒成立,即求函数f(x)的最小值>0即可,利用基本不等式求最值,一定注意等号成立的条件,因此对b进行讨论,当2≤b<4时,f(x)最小值为 ,b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为
,b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为 ,从而求得b的取值范围.
,从而求得b的取值范围.
点评:此题是个中档题.考查利用基本不等式求函数的最值问题,注意正定等,考查了学生灵活应用知识分析解决问题的能力.
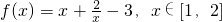 .
.因为f(x)在
 上单调递减,在
上单调递减,在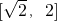 上单调递增,
上单调递增,所以f(x)的最小值为
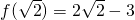 .
.又因为f(1)=f(2)=0,
所以f(x)的值域为
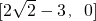 .
.(2)(ⅰ)当2≤b<4时,因为f(x)在
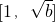 上单调递减,在
上单调递减,在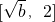 上单调递增,
上单调递增,f(x)最小值为
 ,f(x)>0,即
,f(x)>0,即 .
.得
 .
.(ⅱ)b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为
 ,f(x)>0,
,f(x)>0,即
 ,得b>2,因此b≥4.
,得b>2,因此b≥4.综合(ⅰ)(ⅱ)可知
 .
.分析:(1)当b=2时,
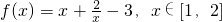 ,利用双钩函数的单调性即可求得f(x)的值域;
,利用双钩函数的单调性即可求得f(x)的值域;(2))b≥2时,f(x)>0恒成立,即求函数f(x)的最小值>0即可,利用基本不等式求最值,一定注意等号成立的条件,因此对b进行讨论,当2≤b<4时,f(x)最小值为
 ,b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为
,b≥4时,f(x)在[1,2]上单调递减,f(x)最小值为 ,从而求得b的取值范围.
,从而求得b的取值范围.点评:此题是个中档题.考查利用基本不等式求函数的最值问题,注意正定等,考查了学生灵活应用知识分析解决问题的能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目