题目内容
(本小题10分)
如图,已知AP是 O的切线,P为切点,AC是
O的切线,P为切点,AC是 O的割线,与
O的割线,与 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。
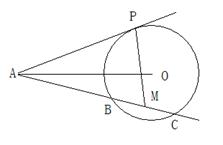
(1) 证明:A,P,O,M四点共圆;
(2) 求 OAM+
OAM+ APM的大小。
APM的大小。
如图,已知AP是
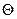 O的切线,P为切点,AC是
O的切线,P为切点,AC是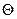 O的割线,与
O的割线,与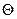 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。
(1) 证明:A,P,O,M四点共圆;
(2) 求
 OAM+
OAM+ APM的大小。
APM的大小。(本小题10分)
(1)证明:如图,连结OP,OM.
∵AP与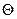 O相切于点P,∴OP⊥AP.
O相切于点P,∴OP⊥AP.
∵点M是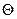 O 的弦BC的中点,∴OM⊥BC。
O 的弦BC的中点,∴OM⊥BC。
于是 OPA+
OPA+ OMA=180°
OMA=180°
即四边形APOM的对角互补
∴A,P,O,M四点共圆
(2)由(1)得A,P,O,M四点共圆
∴ OAM=
OAM= OPM。
OPM。
由(1)得OP⊥AP,由圆心O在 PAC的内部,可知
PAC的内部,可知 OPM+
OPM+ APM=90°
APM=90°
所以 OAM+
OAM+ APM=90°。
APM=90°。
(1)证明:如图,连结OP,OM.
∵AP与
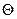 O相切于点P,∴OP⊥AP.
O相切于点P,∴OP⊥AP.∵点M是
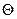 O 的弦BC的中点,∴OM⊥BC。
O 的弦BC的中点,∴OM⊥BC。于是
 OPA+
OPA+ OMA=180°
OMA=180°即四边形APOM的对角互补
∴A,P,O,M四点共圆
(2)由(1)得A,P,O,M四点共圆
∴
 OAM=
OAM= OPM。
OPM。由(1)得OP⊥AP,由圆心O在
 PAC的内部,可知
PAC的内部,可知 OPM+
OPM+ APM=90°
APM=90°所以
 OAM+
OAM+ APM=90°。
APM=90°。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,Q是x轴上的动点,QA、QB分别切圆M于A、B两点。
,Q是x轴上的动点,QA、QB分别切圆M于A、B两点。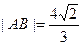 ,求
,求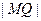 的长;
的长;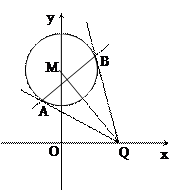 (2)求证:直线AB恒过定点,并求出定点坐标.
(2)求证:直线AB恒过定点,并求出定点坐标. 上,并且经过A(2,1)B(1,2)两点,求圆C的标准方程.
上,并且经过A(2,1)B(1,2)两点,求圆C的标准方程. 经过
经过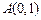 ,
,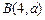
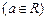 两点
两点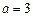 ,并且
,并且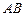 是圆
是圆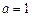 时,圆
时,圆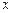 轴相切,求此时圆
轴相切,求此时圆 取何实数,圆
取何实数,圆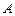 外的另一个定点,求出这个定点坐标
外的另一个定点,求出这个定点坐标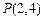 向圆
向圆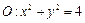 作切线,求切线的方程;
作切线,求切线的方程;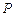 在圆
在圆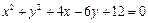 上,点
上,点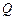 在直线
在直线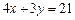 上,求
上,求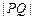 的最小值.
的最小值.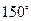 的直线被圆
的直线被圆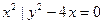 截得的弦长为 。
截得的弦长为 。 和点A(1,2),则过点A且与圆O相切的直线方程为 。
和点A(1,2),则过点A且与圆O相切的直线方程为 。 与圆
与圆 相切,则三条边分别为
相切,则三条边分别为 的三角形是 ( )
的三角形是 ( )