题目内容
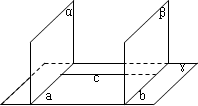
如下图,已知平面α∩β=a, b ?
?
思路分析:反证法.假设b、c共面,则有两种情况:①b与c相交;②b与c平行.?
证法一:假设b、c不是异面直线,即b、c为共面直线,则b、c为相交直线或平行直线.
(1)若b∩c=P,已知b![]() β,c
β,c![]() α,又α∩β=a,则P∈b
α,又α∩β=a,则P∈b![]() β,且P∈c
β,且P∈c![]() α,从而,交点P一定在平面α、β的交线上(公理二),即P∈a,于是a∩c=P,这与已知条件a∥c矛盾.因此b、c相交不成立.?
α,从而,交点P一定在平面α、β的交线上(公理二),即P∈a,于是a∩c=P,这与已知条件a∥c矛盾.因此b、c相交不成立.?
(2)若b∥c,已知a∥c,则a∥b(公理四),这与已知条件a∩b=A矛盾,因此b、c平行也不能成立.?
综合(1)(2)可知b、c为异面直线.?
证法二:假设b、c不是异面直线,即假设直线b、c在同一个平面γ内,则b ![]() γ,c
γ,c![]() γ,在直线b上任取一点B(不同于A,B
γ,在直线b上任取一点B(不同于A,B ![]() α);从而,平面γ一定经过B点与直线c.?
α);从而,平面γ一定经过B点与直线c.?
又∵A∈a,a∥c,?
∴A![]() α.于是c与c外一点A的平面就是α,而这样的平面只能有一个.从而,直线b、c都在平面α内,但B∈b
α.于是c与c外一点A的平面就是α,而这样的平面只能有一个.从而,直线b、c都在平面α内,但B∈b![]() α,这与B
α,这与B![]() α矛盾.因此b、c为异面直线.?
α矛盾.因此b、c为异面直线.?
温馨提示:立体几何中异面直线问题、共面问题常用反证法.反证法中要正确推理,将反设列入已知条件,按一般逻辑推理程序和法则推理.推理中没有用到“反设”就不是反证法.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目

 ,
, ,且
,且 ,
, ,
, ,
, ,
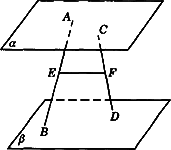
, 是垂足,试判断直线
是垂足,试判断直线 与
与 的位置关系?并证明你的结论.
的位置关系?并证明你的结论.
