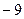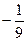题目内容
(本小题满分14分)设函数 . (1) 判断
. (1) 判断 在区间
在区间 上的增减性并证明之;(2) 若不等式
上的增减性并证明之;(2) 若不等式 ≤
≤ ≤
≤ 对
对 恒成立, 求实数
恒成立, 求实数 的取值范围M;(3)设
的取值范围M;(3)设 ≤
≤ ≤
≤ ,若
,若 ,求证:
,求证: ≥
≥ .
.
 . (1) 判断
. (1) 判断 在区间
在区间 上的增减性并证明之;(2) 若不等式
上的增减性并证明之;(2) 若不等式 ≤
≤ ≤
≤ 对
对 恒成立, 求实数
恒成立, 求实数 的取值范围M;(3)设
的取值范围M;(3)设 ≤
≤ ≤
≤ ,若
,若 ,求证:
,求证: ≥
≥ .
.(1)减函数 (2) ≤
≤ ≤
≤ (3)略
(3)略
 ≤
≤ ≤
≤ (3)略
(3)略:(1)∵  ∴
∴ …1分
…1分
设
 则
则 ……2分
……2分
∴ 在
在 上为减函数 又
上为减函数 又
 时,
时,
 ,
,
∴ ∴
∴ 在
在 上是减函数………4分
上是减函数………4分
(2)①∵ ∴
∴ 或
或 时
时
 ∴
∴ ………6分
………6分
又≤ ≤
≤ 对一切
对一切 恒成立 ∴
恒成立 ∴ ≤
≤ ≤
≤ …8分
…8分
②显然当 或
或 时,不等式成立 …9分
时,不等式成立 …9分
(3)当 ,原不等式等价于
,原不等式等价于 ≥
≥ ……10分
……10分
下面证明一个更强的不等式: ≥
≥ …①
…①
即 ≥
≥ ……②亦即
……②亦即 ≥
≥ …11分
…11分
由(1) 知 在
在 上是减函数 又
上是减函数 又 ∴
∴ ……12分
……12分
∴不等式②成立,从而①成立 又

∴ >
> 综合上面∴
综合上面∴ ≤
≤ ≤
≤ 且
且 ≤
≤ ≤
≤ 时,原不等式成立……14分
时,原不等式成立……14分
 ∴
∴ …1分
…1分设

 则
则 ……2分
……2分∴
 在
在 上为减函数 又
上为减函数 又
 时,
时,
 ,
,∴
 ∴
∴ 在
在 上是减函数………4分
上是减函数………4分(2)①∵
 ∴
∴ 或
或 时
时 ∴
∴ ………6分
………6分又≤
 ≤
≤ 对一切
对一切 恒成立 ∴
恒成立 ∴ ≤
≤ ≤
≤ …8分
…8分②显然当
 或
或 时,不等式成立 …9分
时,不等式成立 …9分(3)当
 ,原不等式等价于
,原不等式等价于 ≥
≥ ……10分
……10分下面证明一个更强的不等式:
 ≥
≥ …①
…①即
 ≥
≥ ……②亦即
……②亦即 ≥
≥ …11分
…11分由(1) 知
 在
在 上是减函数 又
上是减函数 又 ∴
∴ ……12分
……12分∴不等式②成立,从而①成立 又


∴
 >
> 综合上面∴
综合上面∴ ≤
≤ ≤
≤ 且
且 ≤
≤ ≤
≤ 时,原不等式成立……14分
时,原不等式成立……14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE=
,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE= ,设△ADE面积为S
,设△ADE面积为S 
 ,并标出定义域。
,并标出定义域。 表示某一时刻一立方米湖水中所含污染物的克数(我们称其为“湖水污染质量分数”),
表示某一时刻一立方米湖水中所含污染物的克数(我们称其为“湖水污染质量分数”), 表示湖水污染初始质量分数.(1)当湖水污染质量分数为常数时,求湖水污染初始质量分数;(2)分析
表示湖水污染初始质量分数.(1)当湖水污染质量分数为常数时,求湖水污染初始质量分数;(2)分析 时,湖水的污染程度如何?
时,湖水的污染程度如何?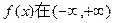 上满足
上满足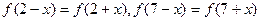 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有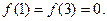


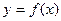 的奇偶性;
的奇偶性;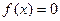 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.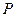 在正方体
在正方体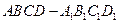 的对角线
的对角线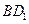 上.过点
上.过点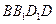 的直线,与正方体表面相交于
的直线,与正方体表面相交于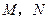 .设
.设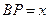 ,
,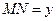 ,则函数
,则函数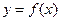 的图象大致是( )
的图象大致是( )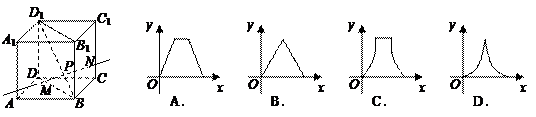
 在(-∞,+∞)上单调递减,则实数a的取值范围是
在(-∞,+∞)上单调递减,则实数a的取值范围是 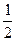 )x的图象关于直线y=x对称,则f(2x-x2)的单调减区间为( )
)x的图象关于直线y=x对称,则f(2x-x2)的单调减区间为( )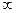 ,1)
,1)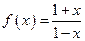 ,又记
,又记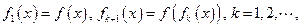
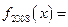 ( )
( )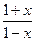 ;
;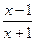 ;
;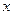 ;
;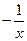 ;
;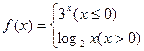 ,那么
,那么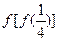 的值为 ( )
的值为 ( )