题目内容
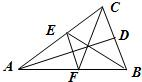
已知D、E、F分别是三条射线SA、SB、SC上的点，且FD与CA交于M，FE与CB交于N，DE与AB交于P,求证:M、N、P三点共线.
证明:∵FD∩CA=M，FE∩CB=N，DE∩AB=P,
∴M、N、P在由D、E、F确定的平面内.
∵M、N、P分别在直线CA、CB、AB上,
∴M、N、P必在平面ABC内,
即M、N、P是平面DEF和平面ABC的公共点.
∴它们在两平面的交线上.
∴M、N、P三点共线.
练习册系列答案
相关题目
已知D、E、F分别是△ABC的边AB、BC、CA的中点，则下列等式中不正确的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
=a，
=b，
=c,则下列各式：①
=
c-
b;②
=a+
b;③
=-
a+
b;④
+
+
=0.
B．
D．
，
，
，则①
，②
，③
，④
中正确的等式的个数为
( )