题目内容
设函数f(x)=4x+cosx,{an}是公差为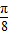 的等差数列,f(a1)+f(a2)+…+f(a5)=10π,则
的等差数列,f(a1)+f(a2)+…+f(a5)=10π,则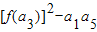 =( )
=( )A.
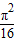
B.
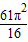
C.
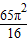
D.无法确定
【答案】分析:由f(x)=4x+cosx,又{an}是公差为 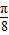 的等差数列,可求得f(a1)+f(a2)+…+f(a5)=20a3+cosa3(1+
的等差数列,可求得f(a1)+f(a2)+…+f(a5)=20a3+cosa3(1+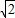 +
+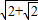 ),可求得a3=
),可求得a3=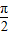 从而可求得答案.
从而可求得答案.
解答:解:∵f(x)=4x+cosx,
∴f(a1)+f(a2)+…+f(a5)=4(a1+a2+…+a5)+(cosa1+cosa2+…+cosa5),
∵{an}是公差为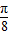 的等差数列,
的等差数列,
∴a1+a2+…+a5=5a3,由和差化积公式可得:cosa1+cosa2+…+cosa5
=(cosa1+cosa5)+(cosa2+cosa4)+cosa3
=[cos(a3-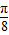 ×2)+cos(a3+
×2)+cos(a3+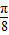 ×2)]+[cos(a3-
×2)]+[cos(a3-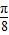 )+cos(a3+
)+cos(a3+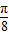 )]+cosa3
)]+cosa3
=2cos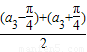 cos
cos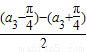 +2cos
+2cos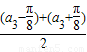 cos
cos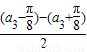 +cosa3
+cosa3
=2cosa3•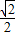 +2cosa3•cos(-
+2cosa3•cos(-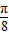 )+cosa3
)+cosa3
=cosa3(1+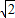 +
+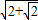 ),
),
∵f(a1)+f(a2)+…+f(a5)=10π,即20a3+cosa3(1+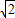 +
+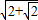 )=10π,
)=10π,
∴cosa3=0,a3=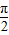
∴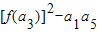 =
=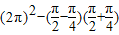 =
=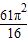
故选B
点评:本题考查数列与三角函数的综合应用,求得cosa3=0,a3= 是关键,也是难点,考查分析,推理与计算能力,属于难题.
是关键,也是难点,考查分析,推理与计算能力,属于难题.
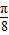 的等差数列,可求得f(a1)+f(a2)+…+f(a5)=20a3+cosa3(1+
的等差数列,可求得f(a1)+f(a2)+…+f(a5)=20a3+cosa3(1+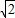 +
+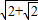 ),可求得a3=
),可求得a3=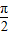 从而可求得答案.
从而可求得答案.解答:解:∵f(x)=4x+cosx,
∴f(a1)+f(a2)+…+f(a5)=4(a1+a2+…+a5)+(cosa1+cosa2+…+cosa5),
∵{an}是公差为
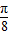 的等差数列,
的等差数列,∴a1+a2+…+a5=5a3,由和差化积公式可得:cosa1+cosa2+…+cosa5
=(cosa1+cosa5)+(cosa2+cosa4)+cosa3
=[cos(a3-
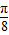 ×2)+cos(a3+
×2)+cos(a3+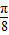 ×2)]+[cos(a3-
×2)]+[cos(a3-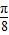 )+cos(a3+
)+cos(a3+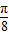 )]+cosa3
)]+cosa3=2cos
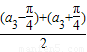 cos
cos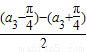 +2cos
+2cos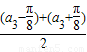 cos
cos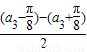 +cosa3
+cosa3=2cosa3•
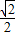 +2cosa3•cos(-
+2cosa3•cos(-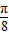 )+cosa3
)+cosa3=cosa3(1+
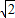 +
+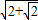 ),
),∵f(a1)+f(a2)+…+f(a5)=10π,即20a3+cosa3(1+
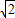 +
+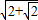 )=10π,
)=10π,∴cosa3=0,a3=
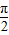
∴
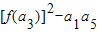 =
=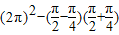 =
=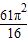
故选B
点评:本题考查数列与三角函数的综合应用,求得cosa3=0,a3=
 是关键,也是难点,考查分析,推理与计算能力,属于难题.
是关键,也是难点,考查分析,推理与计算能力,属于难题. 
练习册系列答案
相关题目
设函数f(x)=
在点x=1处连续,则a等于( )
|
A、-
| ||
B、
| ||
C、-
| ||
D、
|