题目内容

如图，已知两圆内切于P，大圆的弦AB切小圆于C点．

求证：∠1＝∠2．

答案：
解析：

　　证明：过点P作两圆的外公切线MN，如图，因为AB切小圆于C点，

　　所以∠MPC＝∠ACP，∠MPA＝∠B，

　　∠1＝∠MPC－∠MPA．

　　因为∠2＝∠ACP－∠B，

　　所以∠1＝∠2．

　　分析：要证∠1＝∠2，找不到等角的代换与转化，所以作内切两圆的外公切线MN，构造弦切角．

　　利用弦切角定理及其推论的等量关系，通过三角形外角和定理及等式的性质使问题得证．


练习册系列答案
相关题目
（2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
B．选修4-2：矩阵与变换
已知矩阵M=
21
34

（1）求矩阵M的逆矩阵；
（2）求矩阵M的特征值及特征向量；
C．选修4-2：矩阵与变换
在平面直角坐标系x0y中，求圆C的参数方程为
x=-1+rcosθ
y=rsinθ
(θ为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
4
)=2
2
．若直线l与圆C相切，求r的值．
D．选修4-5：不等式选讲
已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：1＜a+b＜
4
3
．

 【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，

             若多做，则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤.

A． 选修4-1：几何证明选讲

   如图，圆与圆内切于点，其半径分别为与，

圆的弦交圆于点（不在上），

求证：为定值。

B． 选修4-2：矩阵与变换

已知矩阵，向量，求向量，使得．

C．选修4-4：坐标系与参数方程

在平面直角坐标系中，求过椭圆（为参数）的右焦点且与直线（为参数）平行的直线的普通方程。

D．选修4-5：不等式选讲

解不等式：

 

如图，线段AB两端点分别在x轴，y轴上滑动，且（）．M为线段AB上一点，且，．

（1）求点M的轨迹的方程；

（2）已知圆O：，设P为轨迹上任一点，若存在以点P为顶点，与圆O外切且内接于轨迹的平行四边形，求证：．
本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
B．选修4-2：矩阵与变换
已知矩阵M=
（1）求矩阵M的逆矩阵；
（2）求矩阵M的特征值及特征向量；
C．选修4-2：矩阵与变换
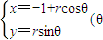在平面直角坐标系x0y中，求圆C的参数方程为为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为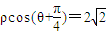．若直线l与圆C相切，求r的值．
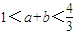D．选修4-5：不等式选讲
已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网