题目内容

求y=sinx+,x∈(0,]的最小值.

   

解：设t=sinx,∵x∈(0,］,

∴t∈(0,1),则y=t+.

    设t1、t2∈(0,1］且t1＜t2,则y1-y2=t1+-t2-=(t1-t2)+=.

∵t1、t2∈(0,1］,∴t1t2-9＜0.

∵0＜t1＜t2≤1,∴t1t2＞0,t1-t2＜0.

∴＞0.∴y1＞y2.

∴y=t+在t∈(0,1)上是减函数.

∴ymin=10,当且仅当t=1即x=时,函数取到最小值.

思维启示：利用基本不等式求最值的关键在于“一正、二定、三相等”,①一正:各项为正;②二定,要求积的最大值,则其和必须为定值,要求和的最值,其积必须为定值;③三相等:必须验证等号是否成立,否则容易导致错误,这一点同学们做题时最容易忽略.


练习册系列答案
相关题目
已知M(1+cos2x，1)，N(1，
3
sin2x+a)（x∈R，a∈R，a是常数），且y=
OM
•
ON
（O为坐标原点）．
（1）求y关于x的函数关系式y=f（x）；
（2）若x∈[0，
π
2
]时，f（x）的最大值为4，求a的值；
（3）在满足（2）的条件下，说明f（x）的图象可由y=sinx的图象如何变化而得到？
已知
a
，
b
是两个向量，且
a
=（1，
3
cosx），
b
=（cos2x，sinx），x∈R，定义：y=
a
•
b
．
（1）求y关于x的函数解析式y=f（x）及其单调递增区间；?
（2）若x∈[0，
π
2
]，求函数y=f（x）的最大值、最小值及其相应的x的值．
已知
a
=（y-m，sinx），
b
=（sinx-2m，1），且
a
∥
b
．
（1）求y关于x的函数关系式y=f（x）；
（2）求函数y=f（x）的最小值g（m）；
（3）若g（m）＞-2，求m的取值范围．
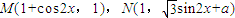已知（x∈R，a∈R，a是常数），且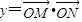（O为坐标原点）．
（1）求y关于x的函数关系式y=f（x）；
（2）若时，f（x）的最大值为4，求a的值；
（3）在满足（2）的条件下，说明f（x）的图象可由y=sinx的图象如何变化而得到？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网