题目内容
已知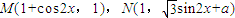 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且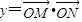 (O为坐标原点).
(O为坐标原点).(1)求y关于x的函数关系式y=f(x);
(2)若
 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;(3)在满足(2)的条件下,说明f(x)的图象可由y=sinx的图象如何变化而得到?
【答案】分析:(1)利用向量的数量积的运算和向量的坐标求得函数的解析式.
(2)利用两角和公式对函数解析式化简整理,根据x的范围确定2x+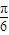 的范围进而利用正弦函数的性质求得函数的最大值,求得a.
的范围进而利用正弦函数的性质求得函数的最大值,求得a.
(3)根据(2)可知f(x)=sin(x+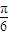 )+2,然后利用三角函数图象平移的法则求得答案.
)+2,然后利用三角函数图象平移的法则求得答案.
解答:解:(1)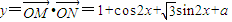 ,
,
所以
(2)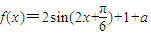 ,
,
因为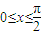 ,所以
,所以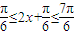 ,
,
当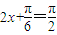 即
即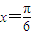 时f(x)取最大值3+a,
时f(x)取最大值3+a,
所以3+a=4,a=1
(3)①将y=sinx的图象向左平移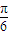 个单位得到函数
个单位得到函数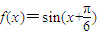 的图象;
的图象;
②将函数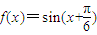 的图象保持纵坐标不变,横坐标缩短为原来的
的图象保持纵坐标不变,横坐标缩短为原来的 得到函数
得到函数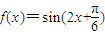 的图象;
的图象;
③将函数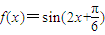 的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数
的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数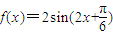 的图象;
的图象;
④将函数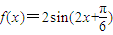 的图象向上平移2个单位,得到函数
的图象向上平移2个单位,得到函数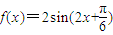 +2的图象
+2的图象
点评:本题主要考查了三角函数的最值,平面向量的数量积的运算,三角函数图象的变换.考查了运用所学知识解决问题的能力.
(2)利用两角和公式对函数解析式化简整理,根据x的范围确定2x+
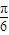 的范围进而利用正弦函数的性质求得函数的最大值,求得a.
的范围进而利用正弦函数的性质求得函数的最大值,求得a.(3)根据(2)可知f(x)=sin(x+
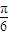 )+2,然后利用三角函数图象平移的法则求得答案.
)+2,然后利用三角函数图象平移的法则求得答案.解答:解:(1)
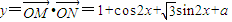 ,
,所以

(2)
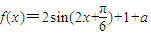 ,
,因为
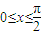 ,所以
,所以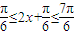 ,
,当
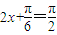 即
即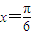 时f(x)取最大值3+a,
时f(x)取最大值3+a,所以3+a=4,a=1
(3)①将y=sinx的图象向左平移
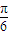 个单位得到函数
个单位得到函数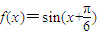 的图象;
的图象;②将函数
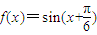 的图象保持纵坐标不变,横坐标缩短为原来的
的图象保持纵坐标不变,横坐标缩短为原来的 得到函数
得到函数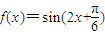 的图象;
的图象;③将函数
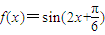 的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数
的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数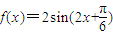 的图象;
的图象;④将函数
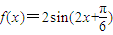 的图象向上平移2个单位,得到函数
的图象向上平移2个单位,得到函数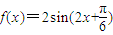 +2的图象
+2的图象点评:本题主要考查了三角函数的最值,平面向量的数量积的运算,三角函数图象的变换.考查了运用所学知识解决问题的能力.

练习册系列答案
相关题目
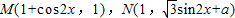 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且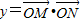 (O为坐标原点).
(O为坐标原点).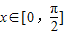 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;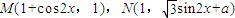 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点).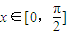 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值; (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点). 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;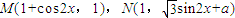 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点).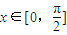 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;