题目内容
已知函数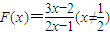
(1)求
 ;
;(2)已知数列{an}满足a1=2,an+1=F(an),求数列{an}的通项公式;
(3) 求证:a1a2a3…an>
 .
.
【答案】分析:(1)根据F(x)的解析式化简得到F(x)+F(1-x)=3,所以把所求的式子乘以2后,倒序相加即可得到所求式子的值;
(2)先把x=an代入f(x)的解析式中,确定出f(an),由an+1=F(an),两边都减去1,化简后即可得到数列 是以2为公差、1为首项得等差数列,写出数列
是以2为公差、1为首项得等差数列,写出数列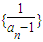 的通项公式即可求出数列{an}的通项公式;
的通项公式即可求出数列{an}的通项公式;
(3)根据(2n)2>(2n)2-1,得到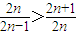 ,根据(2)中求出的数列{an}的通项公式列举出各项,收缩不等式后约分即可得证.
,根据(2)中求出的数列{an}的通项公式列举出各项,收缩不等式后约分即可得证.
解答:解:(1)因为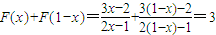 ,
,
所以由倒序相加可得:2[ ]
]
=[F( )+F(
)+F( )]+…+[F(
)]+…+[F(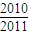 )+F(
)+F( )]
)]
=3×2010=6030,
则 =3015;
=3015;
(2)由an+1=F(an),两边同时减去1,得 ,
,
所以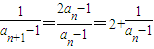 ,
,
故 是以2为公差、1为首项得等差数列.
是以2为公差、1为首项得等差数列.
所以 ,由此
,由此
(3)因为(2n)2>(2n)2-1=(2n+1)(2n-1),
所以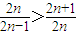 ,于是
,于是
所以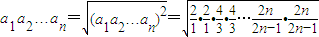
>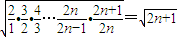 .
.
点评:此题考查了等差数列的通项公式及等差数列的确定方法,是一道中档题.本题的技巧性比较强如第1问中求出F(x)+F(1-x)的值,然后利用倒序相加的方法来求解;第3问证明不等式时注意利用不等式的放缩的方法来证明.
(2)先把x=an代入f(x)的解析式中,确定出f(an),由an+1=F(an),两边都减去1,化简后即可得到数列
 是以2为公差、1为首项得等差数列,写出数列
是以2为公差、1为首项得等差数列,写出数列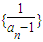 的通项公式即可求出数列{an}的通项公式;
的通项公式即可求出数列{an}的通项公式;(3)根据(2n)2>(2n)2-1,得到
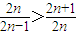 ,根据(2)中求出的数列{an}的通项公式列举出各项,收缩不等式后约分即可得证.
,根据(2)中求出的数列{an}的通项公式列举出各项,收缩不等式后约分即可得证.解答:解:(1)因为
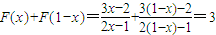 ,
,所以由倒序相加可得:2[
 ]
]=[F(
 )+F(
)+F( )]+…+[F(
)]+…+[F(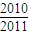 )+F(
)+F( )]
)]=3×2010=6030,
则
 =3015;
=3015;(2)由an+1=F(an),两边同时减去1,得
 ,
,所以
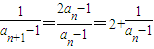 ,
,故
 是以2为公差、1为首项得等差数列.
是以2为公差、1为首项得等差数列.所以
 ,由此
,由此
(3)因为(2n)2>(2n)2-1=(2n+1)(2n-1),
所以
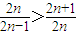 ,于是
,于是
所以
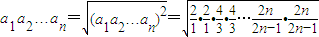
>
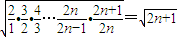 .
.点评:此题考查了等差数列的通项公式及等差数列的确定方法,是一道中档题.本题的技巧性比较强如第1问中求出F(x)+F(1-x)的值,然后利用倒序相加的方法来求解;第3问证明不等式时注意利用不等式的放缩的方法来证明.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目

 的单调递增区间;
的单调递增区间; 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 ,已知
,已知 ,
, 成等差数列,且
成等差数列,且 ,求边
,求边 的值.
的值.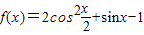
 ,且
,且 ,求sinx的值.
,求sinx的值.
 ,b=1,
,b=1, ,且a>b,试求角B和角C.
,且a>b,试求角B和角C.
 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值; ,求
,求 的值.
的值.