题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ).
).
(Ⅰ)证明:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若数列![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(Ⅰ)证明:由![]() ,
,![]() 时,
时,![]() ,解得
,解得![]() .
.
因为![]() ,则
,则![]()
![]() ,
,
所以当![]() 时,
时,![]() ,
,
整理得![]() .
.
又![]() ,
,
所以![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列. ……………………6分
的等比数列. ……………………6分
(Ⅱ)解:因为![]() ,
,
由![]() ,得
,得![]() .
.
可得![]()
=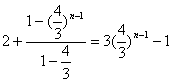 ,(
,(![]() ),
),
当![]() 时也满足,
时也满足,
所以数列![]() 的通项公式为
的通项公式为![]() . ……………………13分
. ……………………13分

练习册系列答案
相关题目
题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ).
).
(Ⅰ)证明:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若数列![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(Ⅰ)证明:由![]() ,
,![]() 时,
时,![]() ,解得
,解得![]() .
.
因为![]() ,则
,则![]()
![]() ,
,
所以当![]() 时,
时,![]() ,
,
整理得![]() .
.
又![]() ,
,
所以![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列. ……………………6分
的等比数列. ……………………6分
(Ⅱ)解:因为![]() ,
,
由![]() ,得
,得![]() .
.
可得![]()
=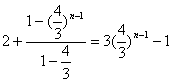 ,(
,(![]() ),
),
当![]() 时也满足,
时也满足,
所以数列![]() 的通项公式为
的通项公式为![]() . ……………………13分
. ……………………13分
