题目内容
6.若关于x的方程$\sqrt{x+1}$-x=m有两个不同的实根,求实数m的取值范围.分析 根据方程的根与对应函数零点之间的关系,可将方程$\sqrt{x+1}$-x=m有两个不同的实根问题转化为函数y=$\sqrt{x+1}$与函数y=x+m的图象有两个交点,我们易求出实数m的取值范围
解答 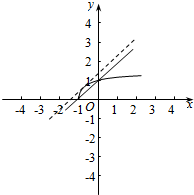 解:方程$\sqrt{x+1}$-x=m有两个不同的实根问题转化为函数y=$\sqrt{x+1}$与函数y=x+m的图象有两个交点,
解:方程$\sqrt{x+1}$-x=m有两个不同的实根问题转化为函数y=$\sqrt{x+1}$与函数y=x+m的图象有两个交点,
由$\sqrt{x+1}$=x+m,两边平方可得x2+(2m-1)x+m2-1=0,
△=(2m-1)2-4(m2-1)=0,可得m=$\frac{5}{4}$,
将(-1,0)代入y=x+m,可得m=1,
∴1≤m<$\frac{5}{4}$.
点评 本题考查的知识点是直线和抛物线的方程的应用,其中根据方程的根与对应函数零点之间的关系,将问题转化为函数的零点问题是解答本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
14.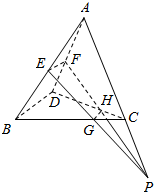 已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
 已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
20.若函数$f(x)={3^{{x^2}-2ax+5}}$在区间(-∞,1]内单调递减,则a的取值范围是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | [1,3) | D. | [1,3] |

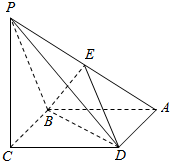 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.