题目内容
已知两定点A(-4,0)、B(4,0),一动点P(x,y)与两定点A、B的连线PA、PB的斜率的乘积为-| 1 | 4 |
分析:欲求点P的轨迹方程,只须寻找它的坐标x,y间的关系式即可,利用题中斜率的乘积为-
列式化简即得.最后将把它化为标准方程,指出是什么曲线即可.
| 1 |
| 4 |
解答:解:∵A(-4,0)、B(4,0),P(x,y)
因为直线PA、PB的斜率存在,所以x≠±4
∴直线PA、PB的斜率分别是k1=
,k2=
.
由题意:PA、PB的斜率的乘积为-
,得:
•
=-
,化简得
+
=1,
∴点P的轨迹的标准方程为
+
=1,x≠±4,
它表示椭圆除去x轴上的两个顶点,
故此曲线为椭圆,除去x轴上的两个顶点.
因为直线PA、PB的斜率存在,所以x≠±4
∴直线PA、PB的斜率分别是k1=
| y |
| x+4 |
| y |
| x-4 |
由题意:PA、PB的斜率的乘积为-
| 1 |
| 4 |
| y |
| x+4 |
| y |
| x-4 |
| 1 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
∴点P的轨迹的标准方程为
| x2 |
| 16 |
| y2 |
| 4 |
它表示椭圆除去x轴上的两个顶点,
故此曲线为椭圆,除去x轴上的两个顶点.
点评:本题考查了轨迹方程、椭圆的定义.直接法:直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
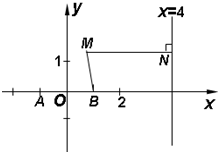 如图,已知两定点A(-1,0),B(1,0)和定直线l:x=4,动点M在直线l上的射影为N,且
如图,已知两定点A(-1,0),B(1,0)和定直线l:x=4,动点M在直线l上的射影为N,且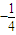 ,求点P的轨迹方程,并把它化为标准方程,指出是什么曲线.
,求点P的轨迹方程,并把它化为标准方程,指出是什么曲线.