题目内容
【题目】甲乙二人进行定点投篮比赛，已知甲、乙两人每次投进的概率均为
，两人各投一次称为一轮投篮．
求乙在前3次投篮中，恰好投进2个球的概率；
设前3轮投篮中，甲与乙进球个数差的绝对值为随机变量
，求的分布列与期望．
【答案】（1）
；（2）
【解析】
利用n次独立重复实验恰有k次发生的概率公式计算即可；
由题意知随机变量
的取值，计算对应的概率值，写出分布列，再求出数学期望值．
乙在前3次投篮中，恰好投进2个球为事件A，
则
；
答：乙在前3次投篮中，恰好投进2个球的概率为；
设前3轮投篮中，甲与乙进球个数差的绝对值为随机变量，
则的取值为0，1，2，3；
设前3轮投篮中，甲进球个数为X，则X的取值为0，1，2，3，
计算
，
，
，
；
所以
，
，
，
；
所以的分布列为；
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望为
练习册系列答案
相关题目
【题目】某银行对某市最近5年住房贷款发放情况(按每年6月份与前一年6月份为1年统计)作了统计调查，得到如下数据：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
贷款 | 50 | 60 | 70 | 80 | 100 |
(1)将上表进行如下处理：
，
得到数据：
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
试求
与
的线性回归方程
，再写出
与
的线性回归方程
.
(2)利用(1)中所求的线性回归方程估算2019年房贷发放数额.
参考公式：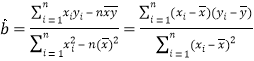
, 
