题目内容
【题目】已知椭圆
（
）的左、右焦点分别为
，
，离心率
，椭圆的短轴长为2.
（1）求椭圆的标准方程；
（2）已知直线
，
过右焦点，且它们的斜率乘积为
，设，分别与椭圆交于点A，B和C，D.
①求
的值；
②设
的中点M，
的中点为N，求
面积的最大值.
【答案】（1）
；（2）①
；②
【解析】
（1）由短轴长为
，得到
，再由离心率结合
计算可得椭圆方程；
（2）①由直线
，
过右焦点
，设出直线的方程与椭圆方程联立，列出韦达定理，计算出弦长，再由两直线的斜率乘积为
，将弦长中的斜率变为
可得弦，相加即可得解；
②由中点坐标公式求出
、
的坐标，观察坐标知
的中点
在
轴上，所以
整理后利用基本不等式即可得到面积的最值；
解：（1）依题意可得
解得
，故椭圆的方程为；
（2）①设的方程为
，
，
联立
消去
并整理得到
，
于是
同理可得
②由①知
，
，
，
，
所以
，
所以的中点
所以
当且仅当
即
时取等号，
所以
面积的最大值为
【题目】艾滋病是一种危害性极大的传染病，由感染艾滋病病毒
病毒
引起，它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标，使人体丧失免疫功能
下表是近八年来我国艾滋病病毒感染人数统计表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
请根据该统计表，画出这八年我国艾滋病病毒感染人数的折线图；
请用相关系数说明：能用线性回归模型拟合y与x的关系；
建立y关于x的回归方程
系数精确到
，预测2019年我国艾滋病病毒感染人数．
参考数据：
；
，
，
，
参考公式：相关系数
，
回归方程
中，
，
．
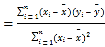【题目】某企业对设备进行升级改造，现从设备改造前后生产的大量产品中各抽取了100件产品作为样本，检测一项质量指标值，若该项指标值落在[20,40)内的产品视为合格品，否则为不合格品，图1是设备改造前样本的频率分布直方图，表1是设备改造后的频数分布表.
表1，设备改造后样本的频数分布表:
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
（1）请估计该企业在设备改造前的产品质量指标的平均数；
（2）企业将不合格品全部销毁后，并对合格品进行等级细分，质量指标值落在[25，30)内的定为一等品，每件售价240元，质量指标值落在[20，25)或[30，35)内的定为二等品，每件售价180元，其它的合格品定为三等品，每件售价120元.根据表1的数据，用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率，现有一名顾客随机购买两件产品，设其支付的费用为X（单位：元），求X得分布列和数学期望.
