题目内容
7．把下列函数分区间表达，并作出函数的图象：（1）f（x）=5-|x|；
（2）f（x）=-5+|x|．
分析 先利用零点分段函数，将函数的解析式化为分段函数的形式，进而画出函数的图象．
解答 解：（1）f（x）=5-|x|=$\left\{\begin{array}{l}5+x，x＜0\\ 5-x，x≥0\end{array}\right.$，其图象如下图所示：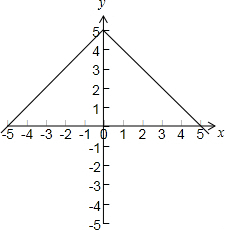
（2）f（x）=-5+|x|=$\left\{\begin{array}{l}-5-x，x＜0\\-5+x，x≥0\end{array}\right.$，其图象如下图所示：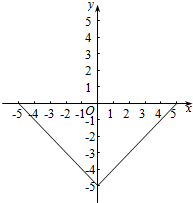
．
点评 本题考查的知识点是分段函数的应用，一次函数的图象和性质，难度中档．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
12．若f（x）=x2+3${∫}_{0}^{1}$f（x）dx，则${∫}_{0}^{1}$f（x）dx=（ ）
| A． | 4 | B． | -6 | C． | -$\frac{1}{6}$ | D． | $\frac{16}{3}$ |