题目内容
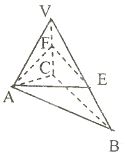
6、正三棱锥V-ABC（顶点在底面的射影是底面正三角形的中心）中，D，E，F分别是VC，VA，AC的中点，P为VB上任意一点，则直线DE与PF所成的角的大小是（ ）
分析：先作一平面VFB，将一直线FP放在一平面VFB内，再证另一直线ED垂直这个面，从而得到两异面直线DE与PF垂直，所以两条异面直线的所成角为90°．
解答：
解：如图，易证ED⊥面VFB，FP?面VFB；
∴ED⊥FP，
故选B．
解：如图，易证ED⊥面VFB，FP?面VFB；∴ED⊥FP，
故选B．
点评：该题主要考查正三棱锥的概念及其异面直线所成的角的计算问题，通过证明线面垂直，得到线线垂直．属于中档题．
练习册系列答案
相关题目
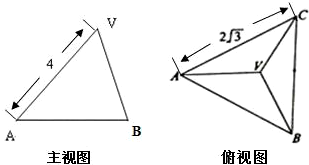已知正三棱锥V-ABC的主视图，俯视图如图所示，其中VA=4，AC=2| 3 |
| A、9 | ||
| B、6 | ||
C、3
| ||
D、
|
如图所示，侧棱长为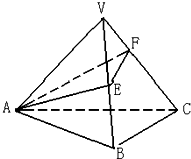
（文科）侧棱长为3