题目内容
已知函数f（x）=tan（2x+
）
（I）求该函数的定义域，周期及单调区间；
（II）若f（θ）=
，求
的值．
| π |
| 4 |
（I）求该函数的定义域，周期及单调区间；
（II）若f（θ）=
| 1 |
| 7 |
2cos2
| ||||
|
（Ⅰ）由题意得，T=
由2x+
≠
+kπ（k∈Z）得，x≠
+
，
由-
+kπ＜2x+
＜
+kπ（k∈Z）得，
-
＜x＜
+
，
综上得，函数的周期是
，定义域是{x|x≠
+
，k∈Z}，
单调增区间是（
-
，
+
）（k∈Z）．
（Ⅱ）式子
=
=
①，
∵f（θ）=
，∴tan（2θ+
）=
，
则tan2θ=tan[（2θ+
）-
]=
=-
，
由tan2θ=
=-
得，tanθ=3或-
，
把tanθ=3代入上式①得，
=-
，
把tanθ=-
代入上式①得，
=2．
| π |
| 2 |
由2x+
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
由-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| 3π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
综上得，函数的周期是
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
单调增区间是（
| kπ |
| 2 |
| 3π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
（Ⅱ）式子
2cos2
| ||||
|
| cosθ-sinθ |
| sinθ+cosθ |
| 1-tanθ |
| tanθ+1 |
∵f（θ）=
| 1 |
| 7 |
| π |
| 4 |
| 1 |
| 7 |
则tan2θ=tan[（2θ+
| π |
| 4 |
| π |
| 4 |
| ||
1+
|
| 3 |
| 4 |
由tan2θ=
| 2tanθ |
| 1-tan2θ |
| 3 |
| 4 |
| 1 |
| 3 |
把tanθ=3代入上式①得，
2cos2
| ||||
|
| 1 |
| 2 |
把tanθ=-
| 1 |
| 3 |
2cos2
| ||||
|
练习册系列答案
相关题目
-1）+lnx，t为常数，且t＞0．
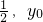）处的切线方程为2x+y-2+ln2，求t和y0的值；
-1）+lnx，t为常数，且t＞0．
）处的切线方程为2x+y-2+ln2，求t和y的值；