题目内容
设sin(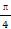 +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )
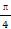 +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )A.- | B.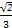 | C. | D.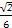 |
A
方法一:利用公式:(sinθ+cosθ)2=1+
2sinθcosθ=1+sin2θ.
由sin( +θ)=
+θ)= ,得
,得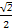 (sinθ+cosθ)=
(sinθ+cosθ)= ,
,
化简得sinθ+cosθ=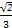 .
.
两边平方得1+sin2θ= .
.
从而sin2θ=- ,
,
方法二:变角利用二倍角余弦公式:cos2θ=1-2sin2θ.
sin2θ=-cos(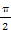 +2θ)
+2θ)
=-cos[2( +θ)]
+θ)]
=2sin2( +θ)-1=-
+θ)-1=- .
.
2sinθcosθ=1+sin2θ.
由sin(
 +θ)=
+θ)= ,得
,得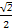 (sinθ+cosθ)=
(sinθ+cosθ)= ,
,化简得sinθ+cosθ=
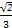 .
.两边平方得1+sin2θ=
 .
.从而sin2θ=-
 ,
,方法二:变角利用二倍角余弦公式:cos2θ=1-2sin2θ.
sin2θ=-cos(
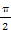 +2θ)
+2θ)=-cos[2(
 +θ)]
+θ)]=2sin2(
 +θ)-1=-
+θ)-1=- .
.
练习册系列答案
相关题目
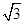 +1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).
+1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).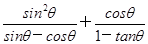 的值;
的值;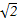 ,π<2θ<2π,化简
,π<2θ<2π,化简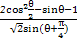 = .
= .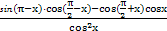 =_________.
=_________.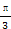 +α)=-
+α)=- ,则sin(α-
,则sin(α-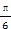 )的值为( )
)的值为( )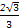
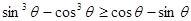 ,且
,且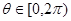 ,则角
,则角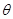 的取值范围是 .
的取值范围是 .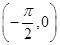 , cos α=
, cos α=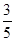 ,则tan
,则tan 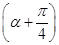 等于( ).
等于( ).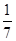
 的值是( )
的值是( )


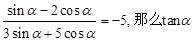 的值为( )
的值为( )