Question

有两点M（-1，0），N（1，0），点P（x，y）使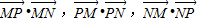成公差小于零的等差数列；
1）求x，y满足的关系式；2）若P横坐标x=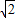，记 θ为夹角，求tanθ值．

Answer 1

【答案】分析：（1）利用向量的坐标运算、数量积运算，将已知化为2x+2+（-2x+2）=2（x²-1+y²），且2x+2＞-2x+2 并整理即可．
（2）利用向量夹角计算公式，先得出cosθ，再求tanθ．
解答：解：（1）由已知，得到：=（x+1，y）   =（2，0）=（x-1，y）
 =-=（-x-1，-y），=-=（-x+1，-y），
∴，
∵成公差小于零的等差数列，
∴2x+2+（-2x+2）=2（x²-1+y²），且2x+2＞-2x+2 整理得出x²+y²=3（x＞0）．
（2）=-=（-x-1，-y），=-=（-x+1，-y），=x²+y²-1=2，===
若P横坐标x=，则==2，cos＜＞==，
θ=45°tanθ=1．
点评：本题考查了向量的坐标运算、数量积运算 向量夹角计算，考查转化、计算能力．