题目内容
函数f(x)=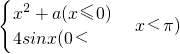
①f(x)在(-∞,π)内连续,则a=________
②若①成立,则集合{x|f(f(x))=0}元素的个数有________.
0 5
分析:①根据f(x)在(-∞,π)内连续建立等式关系,解之即可求出a;
②根据分段函数f(x)解析式,我们结合集合元素要满足的性质f(f (x))=0,易通过分类讨论求了所有满足条件的x的值,进而确定集合中元素的个数.
解答:①∵f(x)在(-∞,π)内连续,
∴f(0)=a=4sin0
即a=0
故答案为:0
②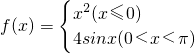
当x≤0时,f(x)=0可得x=0
当0<x≤π时,若f(x)=4sinx=0,则sinx=0,则x=π
当x≤0时,若f(x)=x2=π,则x=- ,
,
当0<x≤π时,若f(x)=4sinx=π,则sinx=
,则x=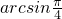 ,
,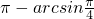
又∵f[f (x)]=0
∴f (x)=0,或f (x)=π
∴x=- ,或x=0,或x=
,或x=0,或x=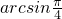 ,或
,或 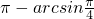 ,或x=π
,或x=π
故答案为:5
点评:本题主要考查了函数的连续性,以及集合中元素的个数及分段函数的函数值,其中根据分段函数的解析式,利用分类讨论的思想构造关于x的方程是解答本题的关键,属于中档题.
分析:①根据f(x)在(-∞,π)内连续建立等式关系,解之即可求出a;
②根据分段函数f(x)解析式,我们结合集合元素要满足的性质f(f (x))=0,易通过分类讨论求了所有满足条件的x的值,进而确定集合中元素的个数.
解答:①∵f(x)在(-∞,π)内连续,
∴f(0)=a=4sin0
即a=0
故答案为:0
②
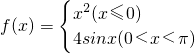
当x≤0时,f(x)=0可得x=0
当0<x≤π时,若f(x)=4sinx=0,则sinx=0,则x=π
当x≤0时,若f(x)=x2=π,则x=-
 ,
,当0<x≤π时,若f(x)=4sinx=π,则sinx=

,则x=
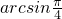 ,
,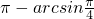
又∵f[f (x)]=0
∴f (x)=0,或f (x)=π
∴x=-
 ,或x=0,或x=
,或x=0,或x=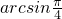 ,或
,或 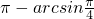 ,或x=π
,或x=π故答案为:5
点评:本题主要考查了函数的连续性,以及集合中元素的个数及分段函数的函数值,其中根据分段函数的解析式,利用分类讨论的思想构造关于x的方程是解答本题的关键,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目