题目内容
已知球O的半径为R,A、B、C为球面上的三点,若任意两点的球面距离均为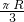 ,则球O的体积与三棱锥O-ABC的体积之比为
,则球O的体积与三棱锥O-ABC的体积之比为
- A.

- B.
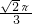
- C.4
 π
π - D.8
 π
π
D
分析:先根据球O的半径为R,A、B、C为球面上的三点,任意两点的球面距离均为 ,可得四面体O-ABC为正四面体
,可得四面体O-ABC为正四面体
过点O作OD⊥平面ABC,垂足为D,连接AD,分别计算球O的体积与三棱锥O-ABC的体积,再求比值.
解答:由题意
∵球O的半径为R,A、B、C为球面上的三点,任意两点的球面距离均为 ,
,

∴∠AOB=∠BOC=∠AOC=
∴四面体O-ABC为正四面体
过点O作OD⊥平面ABC,垂足为D,连接AD,则
∴
∴ =
=
又∵
∴球O的体积与三棱锥O-ABC的体积之比为
故选D.
点评:本题以球为载体,考查球面距离,考查三棱锥的体积、球的体积公式,解题的关键是根据球面距离得出四面体为正四面体.
分析:先根据球O的半径为R,A、B、C为球面上的三点,任意两点的球面距离均为
 ,可得四面体O-ABC为正四面体
,可得四面体O-ABC为正四面体过点O作OD⊥平面ABC,垂足为D,连接AD,分别计算球O的体积与三棱锥O-ABC的体积,再求比值.
解答:由题意
∵球O的半径为R,A、B、C为球面上的三点,任意两点的球面距离均为
 ,
,
∴∠AOB=∠BOC=∠AOC=

∴四面体O-ABC为正四面体
过点O作OD⊥平面ABC,垂足为D,连接AD,则

∴

∴
 =
=
又∵

∴球O的体积与三棱锥O-ABC的体积之比为

故选D.
点评:本题以球为载体,考查球面距离,考查三棱锥的体积、球的体积公式,解题的关键是根据球面距离得出四面体为正四面体.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目