题目内容
已知球面上A、B、C三点的截面和球心的距离都是球半径的一半,且AB=BC=CA=2,则球表面积是
[ ]
A.![]() π
π
B.![]() π
π
C.4π
D.![]() π
π
答案:A
解析:

解析:
解析:如图,过ABC三点的截面圆的圆心是![]() ,球心是O,连结A
,球心是O,连结A![]() 、O
、O![]() ,则O
,则O![]() ⊥A
⊥A![]() .ΔABC中,AB=BC=CA=2,故ΔABC为正三角形.
.ΔABC中,AB=BC=CA=2,故ΔABC为正三角形.

∴A![]() =
=![]() ×2=
×2=![]()
设球半径为R,则OA=R,O![]() =
=![]()
在RtΔOA![]() 中,OA2=
中,OA2=![]() O2+
O2+![]() A2,即R2=
A2,即R2=![]() +(
+(![]()
![]() )2
)2
∴R=![]()
∴球面面积为4πR2=![]() π
π
∴应选A.
说明:因为R=OA>![]() A>
A>![]() AB=1,所以球面积S=4πR2>4π.从而选A.
AB=1,所以球面积S=4πR2>4π.从而选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知过球面上A,B,C三点的截面和球心的距离为球半径的一半,且AB=BC=CA=2,求球的表面积.
已知过球面上A,B,C三点的截面和球心的距离为球半径的一半,且AB=BC=CA=2,求球的表面积. ,且
,且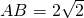 ,
,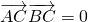 ,则球的表面积是
,则球的表面积是
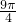
 ,且
,且 ,
, ,则球的表面积是( )
,则球的表面积是( )
