题目内容
已知函数 ,则函数单调递增区间是________.
,则函数单调递增区间是________.
(-∞,-1)和[1,+∞)
分析:函数 可看作函数
可看作函数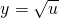 与
与 的复合函数,由复合函数的单调性,要求函数
的复合函数,由复合函数的单调性,要求函数 的增区间只需求函数
的增区间只需求函数 的增区间,因为
的增区间,因为 >0即可解得增区间.
>0即可解得增区间.
解答:由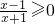 可解得x<-1,或x≥1,即函数的定义域为(-∞,-1)∪[1,+∞)
可解得x<-1,或x≥1,即函数的定义域为(-∞,-1)∪[1,+∞)
函数 可看作函数
可看作函数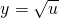 与
与 的复合函数,由复合函数的单调性,
的复合函数,由复合函数的单调性,
要求函数 的增区间只需求函数
的增区间只需求函数 的增区间.
的增区间.
因为 >0即在整个定义域上函数u都是增函数.
>0即在整个定义域上函数u都是增函数.
故已知函数 的增区间为(-∞,-1)和[1,+∞),
的增区间为(-∞,-1)和[1,+∞),
故答案为(-∞,-1)和[1,+∞).
点评:本题为函数增区间的求解,涉及复合函数的单调性和商的导数以及不等式的解法,属中档题.
分析:函数
 可看作函数
可看作函数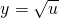 与
与 的复合函数,由复合函数的单调性,要求函数
的复合函数,由复合函数的单调性,要求函数 的增区间只需求函数
的增区间只需求函数 的增区间,因为
的增区间,因为 >0即可解得增区间.
>0即可解得增区间.解答:由
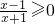 可解得x<-1,或x≥1,即函数的定义域为(-∞,-1)∪[1,+∞)
可解得x<-1,或x≥1,即函数的定义域为(-∞,-1)∪[1,+∞)函数
 可看作函数
可看作函数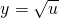 与
与 的复合函数,由复合函数的单调性,
的复合函数,由复合函数的单调性,要求函数
 的增区间只需求函数
的增区间只需求函数 的增区间.
的增区间.因为
 >0即在整个定义域上函数u都是增函数.
>0即在整个定义域上函数u都是增函数.故已知函数
 的增区间为(-∞,-1)和[1,+∞),
的增区间为(-∞,-1)和[1,+∞),故答案为(-∞,-1)和[1,+∞).
点评:本题为函数增区间的求解,涉及复合函数的单调性和商的导数以及不等式的解法,属中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知函数f(x)=cosωx(ω>0),其图象关于点M(
,0)对称,且在区间[0,
]是单调函数,则ω的值为( )
| 6π |
| 7 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 ,则
,则 的单调增区间为 ( )
的单调增区间为 ( ) B.
B. C.
C.  D.
D.