Question

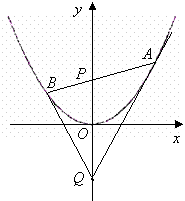
（08年潮州市二模理）（14分）如图,过抛物线的对称轴上任一点作直线与抛物线交于A、B两点，点Q是点P关于原点的对称点．

 ⑴ 设点P满足（为实数），证明：；

⑵ 设直线AB的方程是，过A、B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．

 

Answer 1

解析：解⑴．依题意,可设直线AB的方程为,代入抛物线方程，得：

         ①       ………………………………    ２分

设A、B两点的坐标分别是、，则是方程①的两根，

所以，．　　……………………………………………………   ３分

由点P满足（为实数，），得， 即．

又点Q是点P关于原点的以称点，故点Q的坐标是，从而．

=

 =

 = =0     …………………………  6分

 所以，．   ………………………  7分

 ⑵．由得点A、B的坐标分别是、．

由得，

所以，抛物线在点A处切线的斜率为．　……………  9分

 设圆C的方程是，  

 则            …………………  11分

  解得：．……………………  13分

 所以，圆C的方程是．     ……………  14分