题目内容
已知平面向量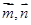 的夹角为
的夹角为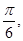 且
且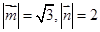 ,在
,在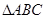 中,
中,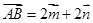 ,
,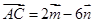 ,
,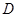 为
为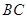 中点,则
中点,则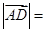 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
A
解析试题分析: ,
,
而 ,
,
∴ .
.
考点:1.向量的数量积定义;2.平行四边形法则;3.求模公式.

练习册系列答案
相关题目
如图,菱形 的边长为
的边长为 ,
, ,
, 为
为 的中点,若
的中点,若 为菱形内任意一点(含边界),则
为菱形内任意一点(含边界),则 的最大值为( )
的最大值为( )
A. | B. | C.9 | D.6 |
已知向量 满足:
满足: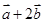 与
与 垂直,且
垂直,且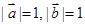 ,则
,则 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知圆 的半径为
的半径为 ,
, 为该圆的两条切线,
为该圆的两条切线, 为两切点,那么
为两切点,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
已知非零向量 和
和 满足
满足 ⊥(
⊥( -
- ),
), ⊥(2
⊥(2 -
- ),则
),则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知两点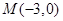 ,
,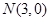 ,点P为坐标平面内一动点,且
,点P为坐标平面内一动点,且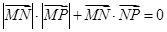 ,则动点
,则动点 到点
到点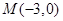 的距离的最小值为( )
的距离的最小值为( )
| A.2 | B.3 | C.4 | D.6 |
已知向量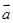 、
、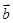 满足
满足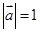 ,
,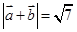 ,
,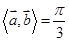 ,则
,则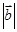 等于 ( )
等于 ( )
A.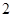 | B. | C.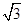 | D.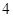 |
已知平面向量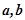 的夹角为
的夹角为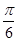 ,且
,且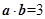 ,
,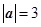 ,则
,则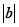 等于( )
等于( )
A. | B.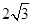 | C.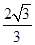 | D. |
在△ABC中,AB=3,AC=2, =
=
 ,则
,则 ·
· 的值为( )
的值为( )
A.- | B. | C.- | D. |