题目内容
已知非零向量 和
和 满足
满足 ⊥(
⊥( -
- ),
), ⊥(2
⊥(2 -
- ),则
),则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
A
解析试题分析:因为 ⊥(
⊥( -
- ),
), ⊥(2
⊥(2 -
- ),所以
),所以 ·(
·( -
- )
)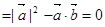 ,
, ·(2
·(2 -
- )
)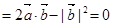 ,即
,即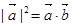 ,
,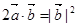 ,所以
,所以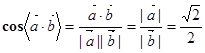 ,所以
,所以 与
与 的夹角为
的夹角为 ,选A.
,选A.
考点:平面向量数量积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知点P(3,3),Q(3,-3),O为坐标原点,动点M(x, y)满足 ,则点M所构成的平面区域的面积是( )
,则点M所构成的平面区域的面积是( )
| A.12 | B.16 | C.32 | D.64 |
已知向量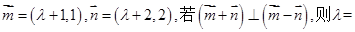 ( )
( )
A.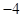 | B.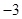 | C.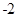 | D.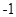 |
已知平面向量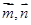 的夹角为
的夹角为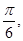 且
且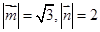 ,在
,在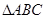 中,
中,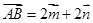 ,
,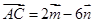 ,
,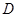 为
为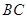 中点,则
中点,则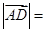 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
已知平面向量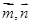 的夹角为
的夹角为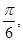 且
且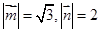 ,在
,在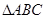 中,
中,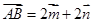 ,
,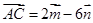 ,
, 为
为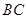 中点,则
中点,则 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
若平面向量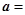
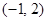 与b的夹角是
与b的夹角是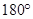 ,且︱
,且︱ ︱
︱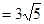 ,则b的坐标为( )
,则b的坐标为( )
A.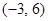 | B. | C.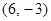 | D. |
已知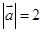 ,
,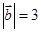 ,
,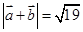 ,则
,则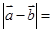 ( )
( )
A.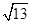 | B.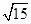 | C.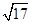 | D.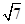 |
平面向量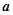 与
与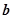 的夹角为60°,
的夹角为60°,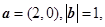 则
则 ( )
( )
A.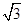 | B.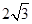 | C.4 | D.12 |
点P是底边长为2 ,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则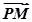 ·
·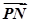 的取值范围是( )
的取值范围是( )
| A.[0,2] | B.[0,3] |
| C.[0,4] | D.[-2,2] |