题目内容
已知等比数列 的各项均为正数,
的各项均为正数, ,
, .
.
(Ⅰ)求数列 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 .证明:
.证明: 为等差数列,并求
为等差数列,并求 的前
的前 项和
项和 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由  ,
, 可求出公比和首项,从而求得通项公式;
可求出公比和首项,从而求得通项公式;
(Ⅱ)由(Ⅰ)得

 ,由等差数列的定义可证得这是一个等差数列,由等差数列求和公式即可得
,由等差数列的定义可证得这是一个等差数列,由等差数列求和公式即可得 的前
的前 项和
项和 .
.
试题解析:(Ⅰ)设等比数列 的公比为
的公比为 ,依题意
,依题意
 .
1分
.
1分
因为  ,
, ,
,
两式相除得  ,
3分
,
3分
解得  ,
舍去
,
舍去  .
4分
.
4分
所以  .
6分
.
6分
所以数列 的通项公式为
的通项公式为  .
7分
.
7分
(Ⅱ)解:由(Ⅰ)得
 =n+1
8分
=n+1
8分
因为  =1
=1
所以数列 是首项为2,公差为d=1的等差数列.
10分
是首项为2,公差为d=1的等差数列.
10分
所以  .
13分
.
13分
考点:等差数列与等比数列.

练习册系列答案
相关题目
 的各项均为正数,公比
的各项均为正数,公比 ,设
,设 ,
, ,则
,则 与
与 的大小关系是
的大小关系是  B.
B. C.
C. D.无法确定
D.无法确定 ,定义数列
,定义数列 为数列
为数列 =2,
=2,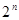 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=
 的各项均为正数,且
的各项均为正数,且 .
. ,求数列
,求数列 的前n项和.
的前n项和. ,求数列{
,求数列{ }的前
}的前 项和.
项和. 的各项均为正数,且
的各项均为正数,且
 ,求数列
,求数列 的前n项和
的前n项和