题目内容
设四边形ABCD中，有
=
且
=
，则这个四边形是（ ）
| AB |
| DC， |
| |AD| |
| |AB| |
分析：由
=
根据向量相等可得出，四边形是平行四边形，由|
|=|
|的几何意义得此四边形邻边相等，从而可判断四边形的形状
| AB |
| DC |
| AB |
| AD |
解答：解：由题意
=
可得出AB
CD，由此得，四边形ABCD是平行四边形
又|
|=|
|
可得此四边形邻边相等，所以此四边形是菱形
故选D
| AB |
| DC |
| ∥ |
. |
又|
| AB |
| AD |
可得此四边形邻边相等，所以此四边形是菱形
故选D
点评：本题考查向量共线与向量相等的几何意义，由此判断出四边形的形状，解题的关键是熟练掌握向量相等与模相等的意义，由向量关系转化出几何关系．
练习册系列答案
相关题目
设四边形ABCD中，有
=
且|
|=|
|，则这个四边形是（ ）
| DC |
| 1 |
| 2 |
| AB |
| AD |
| BC |
| A、平行四边形 | B、矩形 |
| C、等腰梯形 | D、菱形 |
=
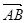，且|
|=|
|，则这个四边形是
=
，且|
|=|
|，则这个四边形是（ ）