题目内容
如图所示的三角形数阵中,第i行第j列的数记为a(i,j),且从第三行起每行都成公比为2的等比数列,则a(20,2)为( )
A.140
B.190
C.210
D.420
【答案】分析:记每一行的第一个数为xn(n∈N*),利用累加法结合等差数列的通项公式,算出xn=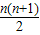 .由此得到第20行的第一个数为a(20,1)=x20=210,再根据从第三行起每行都成公比为2的等比数列,即可算出a(20,2)的值.
.由此得到第20行的第一个数为a(20,1)=x20=210,再根据从第三行起每行都成公比为2的等比数列,即可算出a(20,2)的值.
解答:解:根据题意,记每一行的第一个数为xn,(n∈N*)
可得x2-x1=2,x3-x2=3,x4-x3=4,…,xn-xn-1=n
∴累加可得xn-x1=2+3+4+…+n=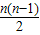 ,得xn=x1+
,得xn=x1+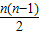 =
=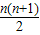
由此得到第20行的第一个数为x20=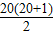 =210=a(20,1)
=210=a(20,1)
又∵从第三行起每行都成公比为2的等比数列,
∴a(20,2)=2a(20,1)=420,
故选:D
点评:本题给出三角形数阵,求第20行的第2个数,着重考查了等差数列的通项与求和、等比数列的定义等知识,属于中档题.
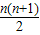 .由此得到第20行的第一个数为a(20,1)=x20=210,再根据从第三行起每行都成公比为2的等比数列,即可算出a(20,2)的值.
.由此得到第20行的第一个数为a(20,1)=x20=210,再根据从第三行起每行都成公比为2的等比数列,即可算出a(20,2)的值.解答:解:根据题意,记每一行的第一个数为xn,(n∈N*)
可得x2-x1=2,x3-x2=3,x4-x3=4,…,xn-xn-1=n
∴累加可得xn-x1=2+3+4+…+n=
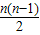 ,得xn=x1+
,得xn=x1+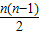 =
=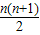
由此得到第20行的第一个数为x20=
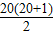 =210=a(20,1)
=210=a(20,1)又∵从第三行起每行都成公比为2的等比数列,
∴a(20,2)=2a(20,1)=420,
故选:D
点评:本题给出三角形数阵,求第20行的第2个数,着重考查了等差数列的通项与求和、等比数列的定义等知识,属于中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
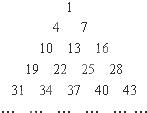 将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )
将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )| A、580 | B、577 | C、576 | D、574 |
 如图所示的三角形数阵叫“莱布尼兹调和三角形”,有
如图所示的三角形数阵叫“莱布尼兹调和三角形”,有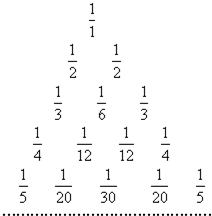 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第b行有n个数,且第n(n≥2)行两端的数均为
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第b行有n个数,且第n(n≥2)行两端的数均为 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( ) 将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是
将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是