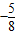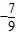题目内容
设 ,
, 是一组非正交的基底,为得到正交基底,可在集合
是一组非正交的基底,为得到正交基底,可在集合 中找一个向量与
中找一个向量与 组成一组正交基底,根据上述要求,若
组成一组正交基底,根据上述要求,若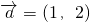 ,
,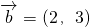 ,则t的值为
,则t的值为
- A.

- B.

- C.
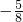
- D.

C
分析:根据所给的两个向量的坐标写出两个向量的数乘与和的表示形式,根据两个向量之间是一组正交基底,得到两个向量的数量积等于0,求出字母的值.
解答:∵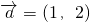 ,
,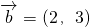 ,
,
∴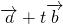 =(1+2t,2+3t),
=(1+2t,2+3t),
∵向量与 组成一组正交基底,
组成一组正交基底,
∴ ,
,
∴(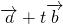 )
) =0,
=0,
∴1+2t+4+6t=0
∴t=-
故选C.
点评:本题考查平面向量的基本定理及其意义,本题解题的关键是求出两个向量的坐标表示,再利用数量积等于0得到结果.
分析:根据所给的两个向量的坐标写出两个向量的数乘与和的表示形式,根据两个向量之间是一组正交基底,得到两个向量的数量积等于0,求出字母的值.
解答:∵
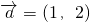 ,
,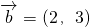 ,
,∴
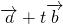 =(1+2t,2+3t),
=(1+2t,2+3t),∵向量与
 组成一组正交基底,
组成一组正交基底,∴
 ,
,∴(
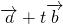 )
) =0,
=0,∴1+2t+4+6t=0
∴t=-

故选C.
点评:本题考查平面向量的基本定理及其意义,本题解题的关键是求出两个向量的坐标表示,再利用数量积等于0得到结果.

练习册系列答案
相关题目
设
,
是一组非正交的基底,为得到正交基底,可在集合{
+t
|t∈R}中找一个向量与
组成一组正交基底,根据上述要求,若
=(1,2),
=(2,3),则t的值为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
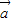 ,
,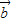 是一组非正交的基底,为得到正交基底,可在集合
是一组非正交的基底,为得到正交基底,可在集合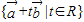 中找一个向量与
中找一个向量与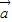 组成一组正交基底,根据上述要求,若
组成一组正交基底,根据上述要求,若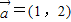 ,
,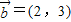 ,则t的值为( )
,则t的值为( )