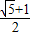题目内容
若F
、F
为双曲线
的左右焦点，O为坐标原点，P在双曲线的左支上，点M在右准线上，且满足；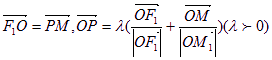
.
（1）求该双曲线的离心率；
（2）若该双曲线过N（2，
），求双曲线的方程；
（3）若过N（2，）的双曲线的虚轴端点分别为B、B（B在y轴正半轴上），点A、B在双曲线上，且
时，直线AB的方程.
（1）
.
（2）所求双曲线的方程为
（3）所求的直线AB的方程为
.
解析:
（1）由
知四边形PF
为平行四边形，∵
（
∴OP平分∠
，∴平行四边形PFOM 为菱形，又∵
∴
.
（2）∵
∴
∴双曲线的方程为
∴所求双曲线的方程为
（3）依题意得
∴
、B
、B共线，不妨设直线AB为：
y=kx-3,A(x
则有
，得
，因为的渐进线为
，当
时，AB与双曲线只有一个交点，不合题意，当
∴
，
又
，∴
∴所求的直线AB的方程为.
练习册系列答案
相关题目
（a>0,b>0）的右准线
一条渐近线
交于两点P、Q，F是双曲线的右焦点。
，求双曲线的方程；
和左支分别为点M、N，若M为PN的中点，求双曲线的离心率e。
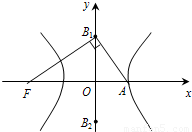
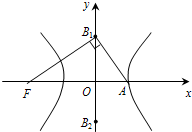如图，F为双曲线
的左焦点，A是它的右顶点，B1B2为虚轴，若∠FB1A=90°，则双曲线的离心率是
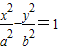的左焦点，A是它的右顶点，B1B2为虚轴，若∠FB1A=90°，则双曲线的离心率是（ ）
