Question

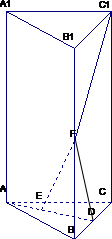
（2012•株洲模拟）已知直三棱柱ABC-A₁B₁C₁，AB=AC，F为BB₁上一点，

BF

FB1

=2，BF=BC=2a，若D为BC的中点，E为线段AD上不同于A，D任意一点．
（1）证明：EF⊥FC₁；
（2）试问：若AB=2a，在线段AD上的E点能否使EF与平面BB₁C₁C成60°角，为什么？证明你的结论．

Answer 1

分析：（1）先证明△FB₁C₁≌△DBF，从而可得C₁F⊥FD，又FD是EF在平面C₁B₁CB的射影，可证C₁F⊥FE；
（2）先证明AD⊥平面C₁B₁CB，可得∠EFD是EF与平面C₁B₁CB所成的角，由FD=

5

a，所以tan60°=

ED

5 a

求出ED长，即可得到结论．

解答：（1）证明：连接FD，FC₁

由

BF

FB1

=2，BF=BC=2a，D为BC的中点，可得BF=B₁C₁，BD=B₁F，
∵∠C₁B₁F=∠FBD，∴△FB₁C₁≌△DBF，则∠C₁FB₁=∠FDB
又∠DFB+∠FDB=90°，所以C₁F⊥FD
又FD是EF在平面C₁B₁CB的射影，则C₁F⊥FE
（2）解：在线段AD上的不存在E点使EF与平面BB₁C₁C成60°角，理由如下：
∵AB=AC，D为BC的中点，
∴AD⊥BC
∵平面ABC⊥平面C₁B₁CB，平面ABC∩平面C₁B₁CB=CB
∴AD⊥平面C₁B₁CB
∴∠EFD是EF与平面C₁B₁CB所成的角
由题意知FD=

5

a，所以tan60°=

ED

5 a

于是ED=

15

a＞

3

a
故不存在．

点评：本题考查线线垂直，考查线面角，考查学生分析解决问题的能力，确定线面角是关键．