题目内容
已知函数
，曲线y=f(x)在x=1处的点的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为
，若
时，y=f(x)有极值．
(1)
求a，b，c的值；（按a,b,c顺序填写)(2)
求y=f(x)在[－3，1]上的最大值和最小值．（先填写最大值，再填写最小值）
答案：2,-4,5;13,95/27
解析：
解析：
|
(1) 由 ，得 ．
当 x=1时，切线l的斜率为3，可得2a＋b=0． ①当  时，y=f(x)有极值，则 ，可得4a＋3b＋4=0． ②
由①②解得 a=2，b=－4．设切线 l的方程为y=3x＋m．由原点到切线 l的距离为 ，则 ．
解得 m=±1．∵切线l不过第四象限，∴m=1．由于切点的横坐标为 x=1，∴f(1)=4．∴1＋a＋b＋c=4．∴c=5；(2) 由(1)可得 ，∴ ．
令  ，得x=－2，．
对应 x的不同区间， 、f(x)的变化趋势如下表：
∴f(x)在x=－2处取得极大值f(－2)=13；在 又f(－3)=8，f(1)=4，∴f(x)在[－3，1]上的最大值为13，最小值为 |
处取得极小值
．
．
练习册系列答案
相关题目
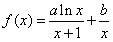，曲线y=f(x)在点(1，f(1))处的切线方程为x+2y-3=0， 
． 
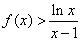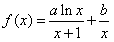，曲线y=f(x)在点(1，f(1))处的切线方程为x+2y-3=0，
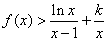，求k的取值范围。 
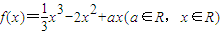在曲线y=f（x）的所有切线中，有且仅有一条切线l与直线y=x垂直．
在曲线y=f（x）的所有切线中，有且仅有一条切线l与直线y=x垂直．
则曲线y=f（x）在点
处的切线方程为 ．