题目内容
“cosα>0”是“x2+y2cosα=1表示焦点在y轴上的椭圆”的( ) 条件.
分析:结合椭圆的方程形式,利用充分条件和必要条件的定义进行判断.
解答:解:若x2+y2cosα=1表示焦点在y轴上的椭圆,则椭圆的标准方程为x2+
=1,此时
>1,所以0<cosα<1.
所以“cosα>0”是“x2+y2cosα=1表示焦点在y轴上的椭圆”的必要不充分条件.
故选C.
| y2 | ||
|
| 1 |
| cosα |
所以“cosα>0”是“x2+y2cosα=1表示焦点在y轴上的椭圆”的必要不充分条件.
故选C.
点评:本题主要考查充分条件和必要条件的应用,要求熟练掌握椭圆的方程和性质.

练习册系列答案
相关题目
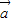 与
与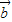 的夹角为α,则cosα<0是
的夹角为α,则cosα<0是 与
与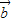 的夹角α为钝角的( )
的夹角α为钝角的( )