题目内容
(本题满分10分)
已知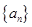 是等差数列,
是等差数列,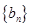 是各项为正数的等比数列,且
是各项为正数的等比数列,且 ,
,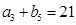 ,
,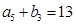 .
.
(Ⅰ)求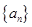 和
和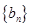 通项公式;
通项公式;
(Ⅱ)若 ,求数列
,求数列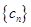 的前
的前 项和
项和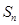 .
.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)设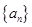 的公差为
的公差为 ,
, 的公比为
的公比为 ,
,
则 ,
,
解得 ,又
,又 ,所以
,所以 …5分
…5分
(Ⅱ) ,
,
所以

两式作差,整理得: . …10分
. …10分
考点:本小题主要考查等差数列和等比数列中基本量的计算,和错位相减法求数列的前 项和,考查学生的运算求解能力.
项和,考查学生的运算求解能力.
点评:错位相减法是求数列的前 项和的重要方法,难在相减后的整理过程容易出错,要仔细整理.
项和的重要方法,难在相减后的整理过程容易出错,要仔细整理.

练习册系列答案
相关题目
已知数列 满足
满足 ,则
,则 等于 ( )
等于 ( )
A. | B.0 | C. | D.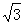 |
在数列 中,
中, 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
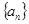 满足:
满足: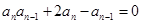 ,
, 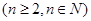 ,
, ,前
,前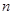 项和为
项和为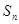 的数列
的数列 满足:
满足: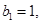
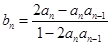
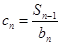
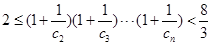
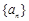 的前n项和为
的前n项和为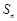 ,点
,点 均在直线
均在直线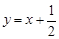 上.
上. 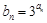 ,试证明数列
,试证明数列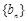 为等比数列.
为等比数列.
 <0.001成立的最小的n值.
<0.001成立的最小的n值.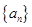 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且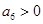 ,
,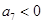 .
. 项和
项和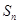 的最大值;
的最大值;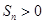 时,求
时,求 的前
的前 项和为
项和为 ,且
,且
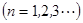 ,等差数列
,等差数列 中,
中, ,
,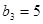 。
。 的通项
的通项 和
和 ;
; ,求数列
,求数列 的前
的前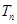 ,
, 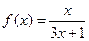 ,数列
,数列 满足
满足
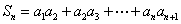 ,求
,求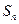 .
.