题目内容
若函数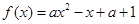 在
在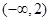 上单调递减,则
上单调递减,则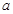 的取值范围是
的取值范围是
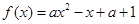 在
在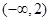 上单调递减,则
上单调递减,则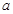 的取值范围是
的取值范围是A. | B. | C. | D. |
C
试题分析:(1)当
 时,函数变为
时,函数变为 ,由一次函数的性质知,
,由一次函数的性质知, 在R上是减函数,符合题意;(2)当
在R上是减函数,符合题意;(2)当 时,
时, ,对称轴为
,对称轴为 ,根据在
,根据在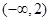 上单调递减,可判断出函数开口向上,
上单调递减,可判断出函数开口向上, 解得:
解得: ;
;综上:
 ,故选:C.
,故选:C.
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
题目内容
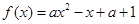 在
在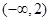 上单调递减,则
上单调递减,则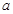 的取值范围是
的取值范围是A. | B. | C. | D. |
 时,函数变为
时,函数变为 ,由一次函数的性质知,
,由一次函数的性质知, 在R上是减函数,符合题意;(2)当
在R上是减函数,符合题意;(2)当 时,
时, ,对称轴为
,对称轴为 ,根据在
,根据在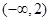 上单调递减,可判断出函数开口向上,
上单调递减,可判断出函数开口向上, 解得:
解得: ;
; ,故选:C.
,故选:C.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案