题目内容

求函数f(x)=x2+2ax-1在区间［0,3］上的最小值.

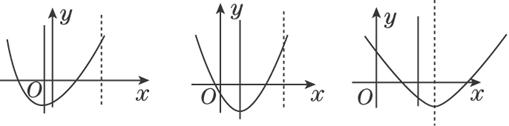
思路解析:讨论函数f(x)=x2+2ax-1在区间［0,3］上的单调性,即可确定函数在区间［0,3］上的最小值.

解:抛物线开口向上,对称轴是x=-a.当x=-a≤0即a≥0时,函数f(x)在区间［0,3］上是单调递增的,∴f(x) min=f(0)=-1.

当0＜-a≤3,即-3≤a＜0时,函数f(x)在区间［0,3］上是先单调递减再单调递增的,∴f(x) min=f(-a)=-a2-1.

当-a＞3即a＜-3时,函数f(x)在区间［0,3］上是单调递减的,∴f(x) min=f(-3)=8+6a.

深化升华

求函数在某闭区间上的最值的问题,实质上是研究函数在该闭区间上的单调性,利用函数在该区间上的单调性判断函数在什么位置取到最值(或区间端点,或区间上某点),从而可以求函数在该闭区间上的单调性.此外,对于有参变量的函数需要注意的是参数对函数图象的影响,并恰当地进行分类讨论.

练习册系列答案
相关题目
求函数f(x)=
x2+x
(x≤-1)的反函数．
求函数f(x)=
x2-2x+2
+
x2-4x+8
的最小值．
（1）已知函数f(x)=
(x+1)0
|x|-x
，求f（-2）的值和函数的定义域
（2）求函数f(x)=
-x2-2x+3
的定义域和值域．
（1）求函数f(x)=
x2-5x+6
+
(x-1)0
x+|x|
的定义域．
（2）求函数y=
x2-x
x2-x+1
的值域．
对定义在实数集R上的函数f1（x），f2（x），令F（x）=f1（x）+f2（x），已知对任意不同的实数x1，x2，|f1（x1）-f1（x2）|＞|f2（x1）-f2（x2）|．
（1）若y=f1（x）是区间D上的增函数，能否确定y=F（x）是区间D上的增函数？若能够确定，说明理由；若不能，请举例说明；
（2）若y=f2（x）是区间D上的增函数，能否确定y=F（x）是区间D上的增函数？若能够确定，说明理由；若不能，请举例说明；
（3）求函数f(x)=x2+
14x
(x＞0)的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网